爱的心脏线

2021-12-5 ~ 2022-11-8
(0)
大一的时候听说了 r = a(1 - cosθ) 这个方程,当时想试着自己推出它的直角坐标系方程,可惜数学不好解不出来,现在感觉编程能力变强了,就试着用程序画出这个方程的图像。这个方程本质上就是一个圆绕着另一个圆转一周时动圆上某个定点的轨迹,看起来像心脏线,而且有数学家笛卡尔与爱徒的故事做背景,这个方程还染上了一丝浪漫的气氛。现在成功用代码把这个爱心方程画出来了。
效果图
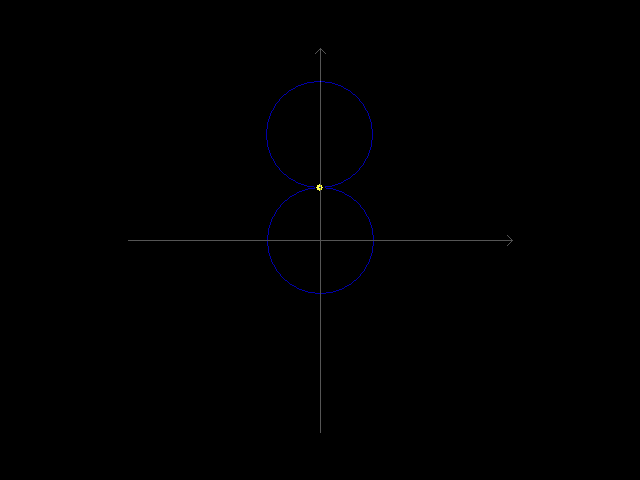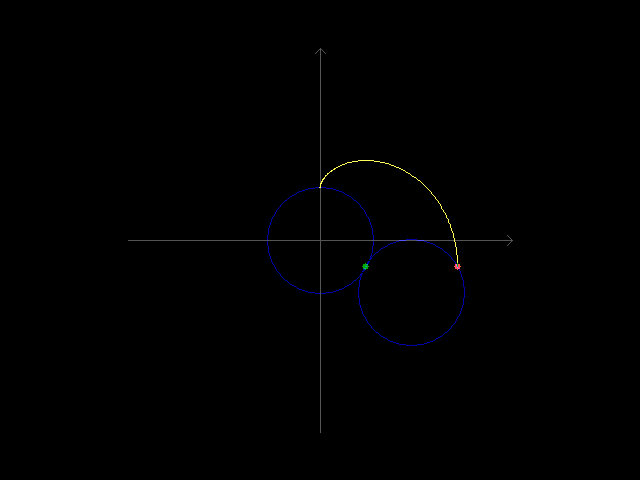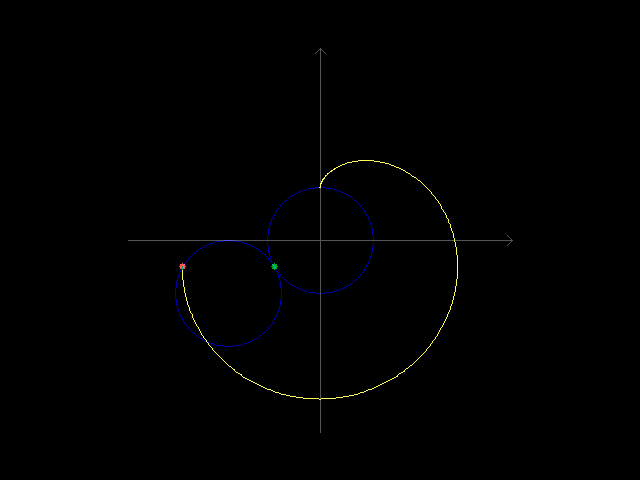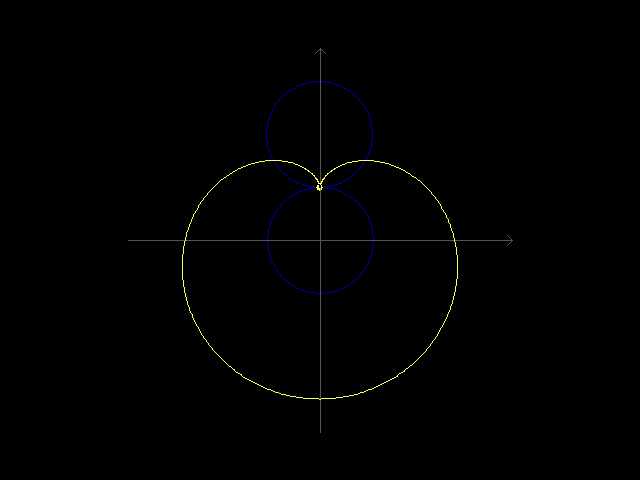
setrop 函数
要写出这个程序,消耗最少的方法是 setrop 函数的 R2_XORPEN 模式,也就是二元光栅的异或模式,绘图时使画上去的颜色和原先的颜色做异或,得到一个与画上去颜色不同但能够经过异或操作得到原先颜色的颜色,方便清除画上去的颜色,虽然不能做到说一不二地让这个像素点打印自己最想要的颜色,不过最终的效果还是很不错的。
要用好这个模式,就得分辨绘制哪些点或者线的时候这个区域的点最终是不希望被改变的,这种区域就不能用 xor 模式,在绘制这些区域的时候就要自动改变为 R2_COPYPEN 模式,然后先把不希望被改变的区域画好接着再画允许随时改变的区域。
例如我这个图像,坐标轴和不动圆以及心脏线是不希望被别人异或改变颜色的,在画这些点或者这些线的时候就用 R2_COPYPEN 模式,反之画动圆,动圆与不动圆的交点以及心脏线当前的点时,这些都是随时会改变的,用 xor 模式时让这些点的区域与不会改变的点的区域进行异或,当这些点被清除时(也就是重新贴上去)再把原来的颜色解密出来。
这种模式可以避免 COPYPEN 模式下要清屏时不停的 cleardevice 造成的屏闪问题,消耗较小。
代码实现
////////////////////////////////////////////
// 程序:心脏线
// 作者:我想做三国志
// 编译环境:Visual Studio 2019,EasyX_20211109
// 编写日期:2022-1-13
#include <graphics.h>
#include <conio.h>
#include <math.h>
#define WIDTH 640 // 窗口宽度
#define HEIGHT 480 // 窗口高度
#define PI 3.14159265 // π
#define DISPLAY 3 // 展示出来动圆与定圆的交点及心脏线当前所在点的尺寸
#define ARROW 5 // 箭头的尺寸
#define COPIES 600 // 份数,看要获得心脏线上的多少个点
#define SECONDS 5 // 跑完一圈的秒数
using namespace std;
// 画坐标抽
void drawCoordinateAxis()
{
setlinecolor(DARKGRAY);
line(WIDTH / 2, HEIGHT / 10, WIDTH / 2, HEIGHT / 10 * 9);
line(WIDTH / 2, HEIGHT / 10, WIDTH / 2 + ARROW, HEIGHT / 10 + ARROW);
line(WIDTH / 2, HEIGHT / 10, WIDTH / 2 - ARROW, HEIGHT / 10 + ARROW);
line(WIDTH / 5, HEIGHT / 2, WIDTH / 5 * 4, HEIGHT / 2);
line(WIDTH / 5 * 4, HEIGHT / 2, WIDTH / 5 * 4 - ARROW, HEIGHT / 2 - ARROW);
line(WIDTH / 5 * 4, HEIGHT / 2, WIDTH / 5 * 4 - ARROW, HEIGHT / 2 + ARROW);
}
int main()
{
initgraph(WIDTH, HEIGHT);
BeginBatchDraw();
setlinecolor(BLUE);
// 画坐标轴,定圆
double r = min(WIDTH, HEIGHT) / 9;
circle(WIDTH / 2, HEIGHT / 2, r);
drawCoordinateAxis();
setrop2(R2_XORPEN);
double lastX = WIDTH / 2.0, lastY = HEIGHT / 2 - r; // 上一个心脏线的点的 x,y 值,初始值为 y 轴正方向上距原点 a 个单位长度的点
for (double a = 0; !_kbhit(); a += PI / COPIES * 2) // a 为当前弧度
{
double x = cos(3.0 / 2.0 * PI + a) * 2 * r + WIDTH / 2; // 动圆这一个循环的圆心的 x 值
double y = sin(3.0 / 2.0 * PI + a) * 2 * r + HEIGHT / 2; // 动圆这一个循环的圆心的 y 值
double FixedPoint_X = cos(PI / 2.0 + a * 2) * r + x; // 当前循环动圆的定点对应的 x 值
double FixedPoint_Y = sin(PI / 2.0 + a * 2) * r + y; // 当前循环动圆的定点对应的 y 值
double Contact_X = cos(PI / 2.0 + a) * r + x; // 当前循环两圆切点在动圆上对应的 x 值
double Contact_Y = sin(PI / 2.0 + a) * r + y; // 当前循环两圆切点在动圆上对应的 y 值
// 画出心脏线,只用画这一个循环的点和上一个循环的点的线就行
setrop2(R2_COPYPEN);
setlinecolor(YELLOW);
line(lastX, lastY, FixedPoint_X, FixedPoint_Y);
setrop2(R2_XORPEN);
lastX = FixedPoint_X;
lastY = FixedPoint_Y;
// 动圆与定圆的切点
setfillcolor(GREEN);
solidcircle(Contact_X, Contact_Y, DISPLAY);
// 心脏线当前点
setfillcolor(LIGHTRED);
solidcircle(lastX, lastY, DISPLAY);
// 动圆
setlinecolor(BLUE);
circle(x, y, r);
FlushBatchDraw();
Sleep((double)(1000 * SECONDS) / (double)COPIES + 0.5);
// 消除动圆
setlinecolor(BLUE);
circle(x, y, r);
// 消除动圆与定圆的交点
setfillcolor(GREEN);
solidcircle(Contact_X, Contact_Y, DISPLAY);
// 消除心脏线当前所在点
setfillcolor(LIGHTRED);
solidcircle(lastX, lastY, DISPLAY);
}
_getch();
EndBatchDraw();
return 0;
}

添加评论
取消回复