实现光栅化渲染 3D 球,平面着色

计算机图形学基础知识
光栅化渲染(Rasterized Rendering)直译过来是栅格化渲染。寻找图像中被几何图形占据的所有像素的过程称为栅格化,因此对象顺序渲染(Object-order rendering)也可以称为栅格化渲染。图形管线(graphics pipeline)是指从几何图形(object)开始到像素更新到屏幕(image,这里理解为屏幕)上的过程。以上是原文,对象顺序渲染我的理解是,对象是指几何图形,例如三角形、四边形、五边形……,将几何图形排序然后挨个渲染就叫对象顺序渲染。图形管线中从几何图形开始我的理解是对几何图形进行操作,例如投影、缩放、剪切。
平面着色(Flat Shading)就是对每一个三维三角形用同一个颜色进行图形管线。
实际操作步骤
1. 栅格化(光栅化)
栅格化也就是找到合适的生成物体表面的三角网的方法。球表面三角网生成的算法图示如下:
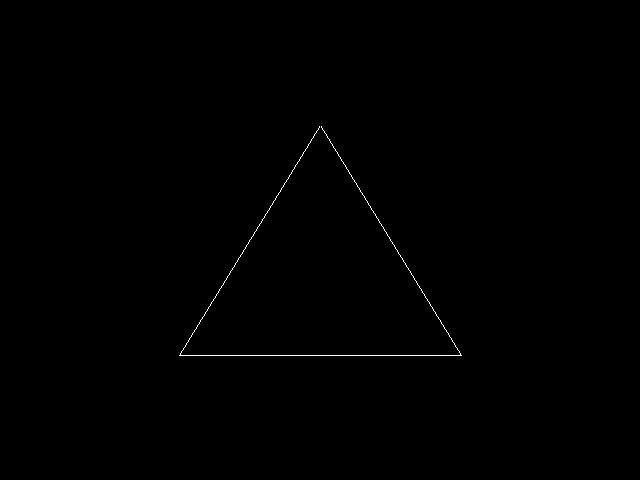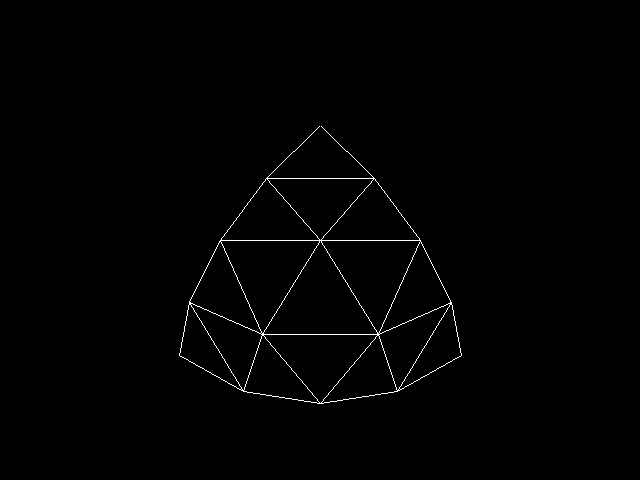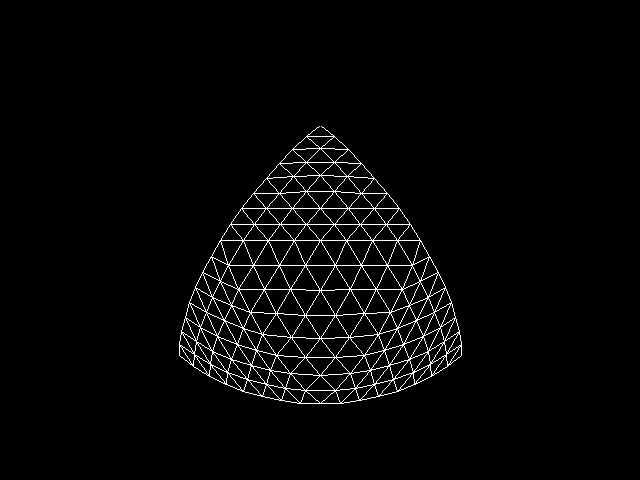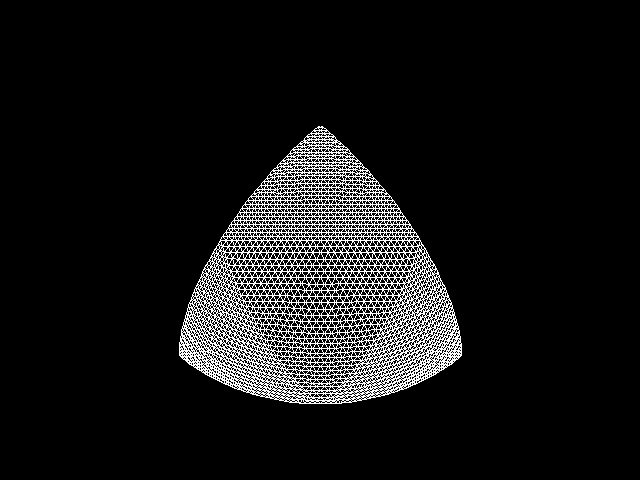
这张图是第一象限的八分之一球表面三角网的生成过程,将球与 X 轴正方向,Y 轴正方向,Z 轴正方向的三个交点作为三维三角形的三个顶点,然后在这个三维三角形上细分出八分之一球面的三角网。这种方法仅对球面有用,无法拓展至其他几何物体上。
接下来给出生成球面上的三角网的算法描述:
1. 生成初始三角网,可以是正四面体,正八面体,正 12 面体。从正八面体开始可以利用对称性将第一象限的三角网对称到其他所有象限。我这里用的是正八面体。
2. 设置三角形队列 TriDeque,将初始三角网的每一个三角形放入队列中,标记入队的三角形数量 TriNum。
3. 遍历 TriDeque 中前 TriNum 个三角形,对每个三角形做如下操作:
①设三个顶点为 a、b、c,球心为 o,对向量 oa, ob 做向量求和操作得到向量 oa_b,对向量 oa, oc 做向量求和得到向量 oa_c,对向量 ob, oc 做向量求和得到向量 ob_c。令向量 oa_b, oa_c, ob_c 的模长变为球的半径,用球心 o 的坐标加上 oa_b, oa_c, ob_c 向量的值得到点 a_b、a_c、b_c 的坐标值。
②添加以 a、a_b、a_c;a_b、b、b_c;a_c、b_c、c;b_c、a_c、a_b;为顶点的四个三角形进 TriDeque 里。注意顺序不能错,三维空间中的三角网一般按从三维物体表面上看逆时针的方向排列点的顺序,这样每个三角形的第一个点依次与每个三角形的第二个、第三个点所构成的向量叉乘一下得到的向量的单位向量就是此三维三角形指向物体表面外侧的法向量。重要的是方向的一致性,即使不保证每个三角形三个顶点的排布顺序为逆时针,也要保证每个三角形三个顶点的排布顺序相同。
③出队当前三角形
4. 目前已经经历过的层数 layers 增加 1 个,判断 layers 是否大于等于所需生成的层数 NeedLayers,是则退出,否则令 TriNum 等于 TriNum * 4,回到第 3 步。
对于球这种特殊的 3d 物体,可以从正八面体开始利用对称性简化运算。对称时注意对称奇数次会导致三维三角形的排布顺序相反。

完成到这一步效果就如上图所示了。
2. 图形管线
图形管线分两步,一是将三角网投影到二维平面上,二是给三角网中的每个三角形上色。
首先需要给每个三维三角形设定颜色值,这个程序设置三维三角形颜色的方法为:
1. 求三维三角形的重心坐标。这一步有公式可以代,设三维三角形三个顶点为 a(x₀, y₀, z₀)、b(x₁, y₁, z₁)、c(x₂, y₂, z₂),则三维三角形的重心坐标为 g((x₀ + x₁ + x₂) / 3, (y₀ + y₁ + y₂) / 3, (z₀ + z₁ + z₂) / 3)。
2. 根据此三维三角形的重心坐标在 xoy 平面的投影的坐标来确定此三维三角形的“经度”。若重心坐标为 g(x₁, y₁, z₁),则重心坐标在 xoy 平面的投影为 g'(x₁, y₁)。设球心为 o(x₀, y₀),得到向量 og(x₁ - x₀, y₁ - y₀) 。以 x 轴正方向的单位向量 X(1, 0) 为经度为 0° 的向量,求 og 与 X 的夹角余弦值,也就是 og * X / (|og| * |X|) 的值。记为 Cos_Tri,若 y₁ - y₀ 小于 0,说明夹角大于 180°,那就令 Cos_Tri 关于 -1 对称,也就是 Cos_Tri = (-1) - (Cos_Tri - (-1)) 化简得 Cos_Tri = -(Cos_Tri + 2)。此时 Cos_Tri 的值在 -3~1 之间分布。伪经度为 pseudo-longitude = Cos_Tri+3,伪经度的范围为 0~4。
3. 根据上一步得到的伪经度求出此三维三角形的色相,这里用 HSB 或者说 HSV 的颜色模型给三角形上色,H 是色相,S 是饱和度,B/V 是亮度,饱和度默认为 1,亮度根据三维三角形平面法向量与光源的余弦值得到,色相在这里设置为 360 * pseudo-longitude / 4,化简得 90 * (Cos_Tri + 3)。
其次要把三维三角形投影到投影面上,一个值是无法确定投影面的,得有两个值才能确定一个投影面,这里用投影面的 x 轴方向单位向量和 y 轴方向单位向量来确定一个投影面。将三维三角形的各个点在这两个单位向量的投影的值设置为三维三角形各个点在投影面上的 x,y 坐标,然后根据这三个坐标填充三角形。
投影面旋转的方法为鼠标横向拖动令 x 轴正方向单位向量绕 y 轴正方向单位向量旋转,鼠标竖向拖动令 y 轴正方向单位向量绕 x 轴正方向单位向量旋转。具体内容在我之前写的《一个正方体》的程序里,可到下方链接详细了解。
最后是设置三角形的亮度,设置一个光源向量 L(x, y, z),x 轴正方向单位向量为 X,y 轴正方向单位向量为 Y,鼠标横向拖动时令 L 绕 Y 旋转,鼠标竖向拖动时令 L 绕 X 旋转。设三维三角形指向球外部的法向量为 normalVec,由于每个三角形三个顶点的排布顺序为表面上看逆时针方向的顺序,所以设三角形三个顶点依次为 a(x₀, y₀, z₀)、b(x₁, y₁, z₁)、c(x₂, y₂, z₂),得到向量 ab(x₁ - x₀, y₁ - y₀, z₁ - z₀)、向量 ac(x₂ - x₀, y₂ - y₀, z₂ - z₀),normalVec 为 ab 与 ac 叉乘的值。叉乘后对 normalVec 进行标准化,也就是 normalVec = normalVec / |normalVec|。接着求 normalVec 与 L 的夹角余弦值 Cos_L,若 Cos_L 大于等于 0 则设置三角形的亮度为 L,若 Cos_L 的值小于 0 则不绘制此三角形。根据色相 H、饱和度 S = 1、亮度 B/V = Cos_L 求出三角形颜色的 RGB 值然后 setfillcolor 接着 solidpolygon 填充三角形。
操作说明
鼠标左键拖动旋转球,右键拖动旋转光源。
程序截图
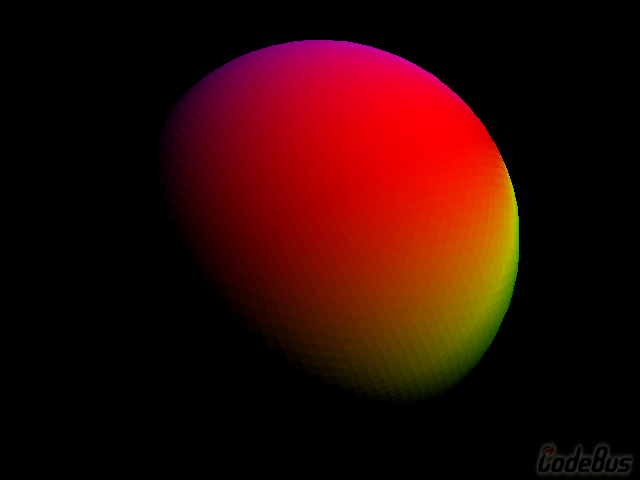
代码实现
////////////////////////////////////////////
// 程序:软光栅渲染一颗 3D 球
// 作者:我想做三国志
// 编译环境:Visual Studio 2022,EasyX_20220901
// 编写日期:2023-3-5
#include <graphics.h>
#include <math.h>
#include <vector>
const double PI = 3.1415926536; // π
const int WIDTH = 640; // 屏幕宽度
const int HEIGHT = 480; // 屏幕高度
const int GAMEPAD = 60; // 游戏手柄,移动多少距离旋转 60°
using std::vector;
// 三维向量
class Vec3
{
public:
double xx, yy, zz;
// 构造函数
Vec3(double xx = 0, double yy = 0, double zz = 0) : xx(xx), yy(yy), zz(zz) {}
// 向量相加
Vec3 operator+(Vec3 num) { return Vec3(this->xx + num.xx, this->yy + num.yy, this->zz + num.zz); }
// 向量乘法
Vec3 operator*(double num) { return Vec3(this->xx * num, this->yy * num, this->zz * num); }
// 向量点乘
double operator*(Vec3 num) { return this->xx * num.xx + this->yy * num.yy + this->zz * num.zz; }
// 向量除法
Vec3 operator/(double num) { return Vec3(this->xx / num, this->yy / num, this->zz / num); }
// 向量相减
Vec3 operator-(Vec3 num) { return Vec3(this->xx - num.xx, this->yy - num.yy, this->zz - num.zz); }
// 得到此向量模长
double GetLength() { return sqrt(this->xx * this->xx + this->yy * this->yy + this->zz * this->zz); }
// 得到两向量之间的 cos 值
double GetCosBetween(Vec3 num) { return (*this) * num / this->GetLength() / num.GetLength(); }
// 得到此向量的单位向量
Vec3 GetUnitVector() { return (*this) / this->GetLength(); }
// 得到此向量在另一个向量上的投影
Vec3 GetProjectionTo(Vec3 num) { return num.GetUnitVector() * (this->GetCosBetween(num) * this->GetLength()); }
// 向量叉乘
Vec3 MultiplicationCross(Vec3 num) { return Vec3(this->yy * num.zz - this->zz * num.yy, -this->xx * num.zz + this->zz * num.xx, this->xx * num.yy - this->yy * num.xx); }
// 求将此向量关于 X 轴,Y 轴,Z 轴旋转 a、b、c 度后的向量
Vec3 GetRotateVec(double a, double b, double c)
{
Vec3 result = this->GetUnitVector();
result = Vec3(result.xx, result.yy * cos(a) - result.zz * sin(a), result.zz * cos(a) + result.yy * sin(a)).GetUnitVector();
result = Vec3(result.xx * cos(b) - result.zz * sin(b), result.yy, result.zz * cos(b) + result.xx * sin(b)).GetUnitVector();
result = Vec3(result.xx * cos(c) - result.yy * sin(c), result.yy * cos(c) + result.xx * sin(c), result.zz ).GetUnitVector();
return (result * this->GetLength());
}
};
// 二维向量
class Vec2
{
public:
double xx, yy;
// 构造函数
Vec2(double xx = 0, double yy = 0) : xx(xx), yy(yy) {}
// 向量相加
Vec2 operator+(Vec2 num) { return Vec2(this->xx + num.xx, this->yy + num.yy); }
// 向量乘法
Vec2 operator*(double num) { return Vec2(this->xx * num, this->yy * num); }
// 向量点乘
double operator*(Vec2 num) { return this->xx * num.xx + this->yy * num.yy; }
// 向量除法
Vec2 operator/(double num) { return Vec2(this->xx / num, this->yy / num); }
// 向量相减
Vec2 operator-(Vec2 num) { return Vec2(this->xx - num.xx, this->yy - num.yy); }
// 得到此向量模长
double GetLength() { return sqrt(this->xx * this->xx + this->yy * this->yy); }
// 得到两向量之间的 cos 值
double GetCosBetween(Vec2 num) { return (*this) * num / this->GetLength() / num.GetLength(); }
// 得到此向量的单位向量
Vec2 GetUnitVector() { return (*this) / this->GetLength(); }
// 得到此向量在另一个向量上的投影
Vec2 GetProjectionTo(Vec2 num) { return num.GetUnitVector() * (this->GetCosBetween(num) * this->GetLength()); }
// 得到此向量旋转 angle 后的向量
Vec2 GetRotateVec(double angle) { return Vec2(this->xx * cos(angle) - this->yy * sin(angle), this->yy * cos(angle) + this->xx * sin(angle)); }
};
// 三维三角形
class Triangle
{
public:
Vec3 a, b, c;
int H;
// H 有 360 个值可取
// L 0~1 根据 cos 值决定
// 构造函数
Triangle() = default;
Triangle(Vec3 a, Vec3 b, Vec3 c, int H = 0) : a(a), b(b), c(c), H(H) {}
};
// 得到三维空间中的点在投影面上的投影
Vec2 GetProjectInSurface(Vec3 project, Vec3 X_Across, Vec3 Y_Across, Vec2 pericenter) // 这个是平行投影
{
return pericenter +
Vec2(project.GetLength() * project.GetCosBetween(X_Across),
project.GetLength() * project.GetCosBetween(Y_Across));
}
// 交换两个值
template<typename T>
void Swap(T& a, T& b)
{
T temp = a;
a = b;
b = temp;
}
// 画填充三角形
void DrawTriangle(Triangle triangle, Vec3 X_Across, Vec3 Y_Across, Vec2 pericenter, double extent, double saturate = 1)
{
if (extent < 0 || extent > 1) return;
Vec2 a = GetProjectInSurface(triangle.a, X_Across, Y_Across, pericenter);
Vec2 b = GetProjectInSurface(triangle.b, X_Across, Y_Across, pericenter);
Vec2 c = GetProjectInSurface(triangle.c, X_Across, Y_Across, pericenter);
COLORREF col = HSVtoRGB(triangle.H, saturate, extent);
POINT pointArr[3] = { {a.xx, a.yy}, {b.xx, b.yy }, {c.xx, c.yy} };
setfillcolor(col);
solidpolygon(pointArr, 3);
}
// 矩阵乘法,其实只是向量之间一一对应相乘得到另一个向量
Vec3 MartixMultiple(Vec3 a, Vec3 b)
{
return Vec3(a.xx * b.xx, a.yy * b.yy, a.zz * b.zz);
}
// 将三维三角形颠倒,也就是此三维三角形关于 xoy 平面,xoz 平面,yoz 平面对称的另一个三维三角形
Triangle ReversedTriangle(Triangle input, Vec3 dir)
{
return Triangle(MartixMultiple(input.a, dir), MartixMultiple(input.b, dir), MartixMultiple(input.c, dir), input.H);
}
// 生成三角网,根据球面生成三角网,radius 是半径,layers 是层数,这个三角网生成跟谢宾斯基三角形有一点点像,最终生成的三角网数量是 8 * 4^(layers) 个,五层就接近一万个了
vector<Triangle> GenerateTriangleMesh(double radius, int layers)
{
vector<Triangle> parent;
vector<Triangle> child;
parent.push_back(Triangle(Vec3(1, 0, 0), Vec3(0, 1, 0), Vec3(0, 0, 1)));
for (int i = 0; i < layers; i++)
{
for (Triangle i : parent)
{
Vec3 a_b = (i.a + i.b).GetUnitVector();
Vec3 a_c = (i.a + i.c).GetUnitVector();
Vec3 b_c = (i.b + i.c).GetUnitVector();
child.push_back(Triangle(i.a, a_b, a_c));
child.push_back(Triangle(a_b, i.b, b_c));
child.push_back(Triangle(a_c, b_c, i.c));
child.push_back(Triangle(b_c, a_c, a_b));
}
parent = child;
child.clear();
}
Vec2 beginDir(1, 0);
for (Triangle& i : parent)
{
Triangle temp_1 = Triangle(i.a * radius, i.b * radius, i.c * radius);
Triangle temp_2 = Triangle(i.a * radius, i.c * radius, i.b * radius);
Triangle triArr[8] = { ReversedTriangle(temp_1, Vec3(1, 1, 1)), ReversedTriangle(temp_2, Vec3(-1, 1, 1)),
ReversedTriangle(temp_2, Vec3(1, -1, 1)), ReversedTriangle(temp_2, Vec3(1, 1, -1)),
ReversedTriangle(temp_1, Vec3(-1, -1, 1)), ReversedTriangle(temp_1, Vec3(1, -1, -1)),
ReversedTriangle(temp_1, Vec3(-1, 1, -1)), ReversedTriangle(temp_2, Vec3(-1, -1, -1)) };
for (int index = 0; index < 8; index++)
{
double XNUM = (triArr[index].a.xx + triArr[index].b.xx + triArr[index].c.xx) / 3.0;
double YNUM = (triArr[index].a.yy + triArr[index].b.yy + triArr[index].c.yy) / 3.0;
Vec2 triVec(XNUM, YNUM);
// 求得 cos 值,根据 y 正负判断是否关于 -1 对称
double Cos_Tri = triVec.GetCosBetween(beginDir);
if (triVec.yy < 0) // Cos_Tri 关于 -1 对称
Cos_Tri = -(Cos_Tri + 2);
triArr[index].H = 90 * (Cos_Tri + 3);
triArr[index].a = triArr[index].a.GetRotateVec(PI / 4.0, PI / 4.0, PI / 4.0);
triArr[index].b = triArr[index].b.GetRotateVec(PI / 4.0, PI / 4.0, PI / 4.0);
triArr[index].c = triArr[index].c.GetRotateVec(PI / 4.0, PI / 4.0, PI / 4.0);
child.push_back(triArr[index]);
}
}
return child;
}
// 鼠标横向拖动时 X 轴,Y 轴关于 Y 轴旋转
Vec3 HorizontalRotate(Vec3 X_Across, Vec3 Y_Across, double angle)
{
Vec3 Z_Across = X_Across.MultiplicationCross(Y_Across);
X_Across = X_Across * cos(angle) + Z_Across * sin(angle);
return X_Across.GetUnitVector();
}
// 鼠标竖向拖动时 X 轴,Y 轴关于 X 轴旋转
Vec3 VerticalRotate(Vec3 X_Across, Vec3 Y_Across, double angle)
{
Vec3 Z_Across = X_Across.MultiplicationCross(Y_Across);
Y_Across = Y_Across * cos(angle) + Z_Across * sin(angle);
return Y_Across.GetUnitVector();
}
// 绘画三角形集合
void DrawTriangleSet(vector<Triangle> triangleSet, Vec3 X_Across, Vec3 Y_Across, Vec2 pericenter,
Vec3* lightsource = nullptr, double saturate = 1)
{
Vec3 Z_Across = X_Across.MultiplicationCross(Y_Across);
for (Triangle& tri : triangleSet)
{
Vec3 normalVec = (tri.b - tri.a).MultiplicationCross(tri.c - tri.a).GetUnitVector();
double extent = normalVec * Z_Across;
if (lightsource == nullptr && extent > 0)
DrawTriangle(tri, X_Across, Y_Across, pericenter, extent, saturate);
else if (lightsource != nullptr && extent > 0)
DrawTriangle(tri, X_Across, Y_Across, pericenter, max(normalVec * (*lightsource), 0), saturate);
}
}
// 旋转三维三角形
void RotateTriangle(Triangle& tri, double a, double b, double c)
{
tri.a = tri.a.GetRotateVec(a, b, c);
tri.b = tri.b.GetRotateVec(a, b, c);
tri.c = tri.c.GetRotateVec(a, b, c);
}
// 旋转三角形集合
void RotateTriangleSet(vector<Triangle>& triSet, double a, double b, double c)
{
for (Triangle& i : triSet)
{
RotateTriangle(i, a, b, c);
}
}
// 主函数
int main()
{
Vec3 X_Across(1, 0, 0), Y_Across(0, 1, 0);
Vec3 lightSource(sqrt(3) / 3, -sqrt(3) / 3, sqrt(3) / 3);
vector<Triangle> triangleMesh = GenerateTriangleMesh(200, 5);
RotateTriangleSet(triangleMesh, PI / 4, PI / 4, PI / 4);
initgraph(WIDTH, HEIGHT);
BeginBatchDraw();
bool isExit = false;
bool isLPress = false, isRPress = false;
double saturate = 1;
Vec2 ori_L, ori_R;
ExMessage msg;
while (!isExit)
{
while (peekmessage(&msg, EM_KEY | EM_MOUSE))
{
if (msg.message == WM_KEYDOWN)
{
if (msg.vkcode == VK_ESCAPE) isExit = true;
}
else if (msg.message == WM_MOUSEMOVE || msg.message == WM_LBUTTONDOWN ||
msg.message == WM_RBUTTONDOWN || msg.message == WM_LBUTTONUP || msg.message == WM_RBUTTONUP)
{
if (!isLPress && msg.lbutton)
{
ori_L = Vec2(msg.x, msg.y);
isLPress = true;
}
else if (isLPress && msg.lbutton)
{
Vec2 next = Vec2(msg.x, msg.y);
ori_L = next - ori_L;
double Th = 0;
double Fi = 0;
Th = ori_L.xx / GAMEPAD * PI / 3;
Fi = ori_L.yy / GAMEPAD * PI / 3;
X_Across = HorizontalRotate(X_Across, Y_Across, Th);
Y_Across = VerticalRotate(X_Across, Y_Across, Fi);
ori_L = next;
}
else if (isLPress && !msg.lbutton)
{
isLPress = false;
}
else if (!isRPress && msg.rbutton)
{
ori_R = Vec2(msg.x, msg.y);
isRPress = true;
}
else if (isRPress && msg.rbutton)
{
Vec2 next = Vec2(msg.x, msg.y);
ori_R = next - ori_R;
// 横向绕 y 轴,竖向绕 x 轴
// 先投影,再旋转
double Th = 0;
double Fi = 0;
Th = ori_R.xx / GAMEPAD * PI / 3;
Fi = ori_R.yy / GAMEPAD * PI / 3;
ori_R = next;
Vec3 Z_Across = X_Across.MultiplicationCross(Y_Across);
Vec2 projectPoint = GetProjectInSurface(lightSource, Z_Across, X_Across, Vec2(0, 0));
projectPoint = projectPoint.GetRotateVec(Th);
lightSource = lightSource.GetProjectionTo(Y_Across) + Z_Across * projectPoint.xx + X_Across * projectPoint.yy;
projectPoint = GetProjectInSurface(lightSource, Z_Across, Y_Across, Vec2(0, 0));
projectPoint = projectPoint.GetRotateVec(Fi);
lightSource = lightSource.GetProjectionTo(X_Across) + Z_Across * projectPoint.xx + Y_Across * projectPoint.yy;
}
else if (isRPress && !msg.rbutton)
{
isRPress = false;
}
}
}
cleardevice();
DrawTriangleSet(triangleMesh, X_Across, Y_Across, Vec2(WIDTH / 2, HEIGHT / 2), &lightSource, saturate);
FlushBatchDraw();
}
return 0;
}

添加评论
取消回复