凸包算法可视化

2022-8-12 ~ 2022-8-18
(1)
程序截图

操作方法
鼠标左键添加点,右键删除点,空格开始运行动画效果。
简单说明
凸包概念
- 点集 Q 的凸包(convex hull)是指一个最小凸多边形,满足 Q 中的点或者在多边形边上或者在其内。
- 一组平面上的点,求一个包含所有点的最小的凸多边形,这就是凸包问题了。这可以形象地想成这样:在地上放置一些不可移动的木桩,用一根绳子把他们尽量紧地圈起来,并且为凸边形,这就是凸包了。
数学定义:设 S 为欧几里得空间 Rn 的任意子集。包含 S 的最小凸集称为 S 的凸包,记作 conv(S)。
算法描述
凸包算法首先要找到最左边或者最下边或者最上边或者最右边的一个点,然后求这个点与其他点的连线与某条基线所形成的夹角,对基线的要求是过起点且所有其他点在线的一侧,根据夹角大小由小到大将点排列起来,然后挨个连起来,在连接的过程中如果下一个点偏转的方向与之前的点偏转的方向不同,就删掉此时这个点,并且重新判断上一个点需不需要删除,直到所有点都判断完。
首先解决判断方向的问题,说得形象点就是判断到达下一个点是要向左拐还是向右拐,这个抽象的问题其实可以转化为判断一个点是在某条线的上方还是下方,看下图:
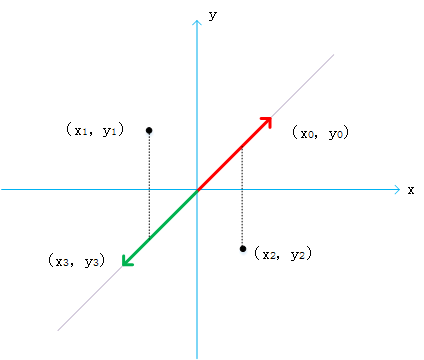
x 大于 0 时在线上方的点在向量的左边,x 小于 0 时在线上方的点在向量的右边
当向量方向向右边时,下一个点在线上方则下一个点在向量左边,当向量方向向左边时,下一个点在线上边则下一个点在向量右边。
此时判断下一个点的方向只需判断点在线上方还是在线下方,由于用向量代替了线,所以线是过原点的,也就是线的方程为 y=kx,令 x = x1 得 y = kx1,若 y1 > kx1 则点在线上方,k = y0 / x0。
① x0 > 0,y1 > kx1 即 y1x0 - x1y0 > 0,此时向量向右,点在线上方,也就是点在向量左边。
② x0<0,y1 > kx1 即 y1x0 - x1y0 < 0,此时向量向左,点在线上方,也就是点在向量右边,若令点在向量左边则 y1x0 - x1y0 > 0。
综上,若下一个点(x1,y1)在向量(x0,y0)左边则,y1x0 - x1y0 > 0,若下一个点在向量右边则,y1x0 - x1y0 < 0。
代码实现
////////////////////////////////////////////
// 程序:凸包算法可视化
// 作者:我想做三国志
// 编译环境:Visual Studio 2019,EasyX_20211109
// 编写日期:2022-8-15
#include<graphics.h>
#include<vector>
#include<math.h>
#define WIDTH 640
#define HEIGHT 480
#define RADIUS 5
using std::vector;
// 对于点来说 x y 是坐标,对于向量来说,x y 是 x 轴 y 轴分向量
struct Point
{
double x, y;
};
typedef Point Vec2;
// 向量的加减乘
Vec2 operator+(Vec2 a, Vec2 b)
{
return { a.x + b.x, a.y + b.y };
}
Vec2 operator-(Vec2 a, Vec2 b)
{
return { a.x - b.x, a.y - b.y };
}
Vec2 operator*(Vec2 num, double times)
{
return { num.x * times, num.y * times };
}
// 获取点 a 到 点 b 的距离
double GetLength(Point a, Point b)
{
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
// 获取起点到终点的向量与基线 x = 0 的余弦值,以便根据次余弦值对点集进行排列
double GetCosAngle(Point begin, Point end)
{
return (end.y - begin.y) / GetLength(begin, end);
}
// 交换点集中的两个位置
void swap(vector<Point>& arr, int index_1, int index_2)
{
Point temp = arr[index_1];
arr[index_1] = arr[index_2];
arr[index_2] = temp;
}
void Line(Point a, Point b)
{
line(a.x, a.y, b.x, b.y);
}
// 线的动画效果
void AnimateLine(Point Begin, Point End, double delaytime, double FPS = 1 / 20.0)
{
Vec2 AllAdd = End - Begin;
for (int i = 0; i <= delaytime / FPS; i++)
{
Point temp = Begin + AllAdd * (i * FPS / delaytime);
Line(Begin, temp);
Sleep(1000 * FPS);
}
}
// 画点集
void DrawPointSet(vector<Point>& pointset)
{
cleardevice();
for (Point i : pointset)
{
solidcircle(i.x, i.y, RADIUS);
}
}
// 判断坐标是否在点集内
bool isInPointSet(vector<Point>& pointset, double x, double y)
{
for (Point i : pointset)
{
if (GetLength(i, { x, y }) < RADIUS)return true;
}
return false;
}
// 凸包算法以及凸包算法可视化的部分
vector<Point> ConvexHullAlgorithm(vector<Point>& pointset)
{
if (pointset.size() <= 1)return pointset; // 只有一个点或没有点直接返回原来的点集
DrawPointSet(pointset); // 先刷新一次,把上一次的线条都擦掉
// 点栈,或许叫点栈缓冲区,将点排列完放到这里后从这里一个一个取出点,入栈,
// 入栈之前判断一下下一个点的放下与其他点的方向相不相同,不相同就把这一个点出栈继续判断下一个点
// 为了避免影响到原来的点集才有了这个点栈
vector<Point>pointstack;
int index = 0; // 最左边的点的下标
for (int i = 0; i < pointset.size(); i++) // 寻找最左边的点并获取最左边的点的下标
{
if (pointset[i].x < pointset[index].x)index = i;
}
pointstack.push_back(pointset[index]); // 将最左边的点放入点栈中
// 根据最左边的点与其他点的连线与 x = 0 这条基线的余弦值大小升序排列点集(point set)并将排列好的点
// 存入点栈(point stack)中
for (int i = 0; i < pointset.size(); i++)
{
if (i == index)continue;
pointstack.push_back(pointset[i]); // 将这个点放入点栈
double CosAngle = GetCosAngle(pointset[index], pointset[i]); // 求这个点与最左边的点的连线与基线的夹角
int temp = pointstack.size() - 1; // 得到点栈最后一个点也就是点集当前这个点
// 用插入排序将当前找到的点放入点栈
while (GetCosAngle(pointset[index], pointstack[temp - 1]) < CosAngle && temp > 1)
{
swap(pointstack, temp, temp - 1);
temp--;
}
}
// parent 是上一个点到这一个点的向量,child 是这一个点到下一个点的向量,
// 点栈中头两个和最后一个点必定在凸包上,所以少判断两次
Vec2 parent = pointstack[1] - pointstack[0], child;
setlinecolor(WHITE);
AnimateLine(pointstack[0], pointstack[1], 1);
for (int i = 1; i < pointstack.size() - 1; i++)
{
child = pointstack[i + 1] - pointstack[i];
setlinecolor(WHITE);
AnimateLine(pointstack[i], pointstack[i + 1], 1); // 将这一个点与下一个点用白线连起来
if (parent.x * child.y - parent.y * child.x > 0) // 下一个点的方向跟其他点的方向不同,说明这个点不属于凸包
{
// 擦掉线和点
setlinestyle(PS_SOLID, 4);
setlinecolor(getbkcolor());
AnimateLine(pointstack[i - 1], pointstack[i], 0.5);
AnimateLine(pointstack[i], pointstack[i + 1], 0.5);
setfillcolor(getbkcolor());
solidcircle(pointstack[i].x, pointstack[i].y, RADIUS);
// 重新画这个点的上一个点和下一个点,因为刚才擦掉线的时候擦到了这两个点
setfillcolor(RED);
solidcircle(pointstack[i - 1].x, pointstack[i - 1].y, RADIUS);
solidcircle(pointstack[i + 1].x, pointstack[i + 1].y, RADIUS);
// 让上上一条线从红色变为白色,因为这个点不属于凸包,所以不能确定上一个点是不是属于凸包,
// 下一次循环从上一个点开始判断
setlinestyle(PS_SOLID, 2);
setlinecolor(WHITE);
AnimateLine(pointstack[i - 1], pointstack[i - 2], 1);
parent = pointstack[i - 1] - pointstack[i - 2];
pointstack.erase(pointstack.begin() + i); // 删除掉这个点
// 以上代码实现了动画效果和删除点的操作
// 刷新画面,避免出现白点
setlinecolor(RED);
DrawPointSet(pointstack);
i -= 2;
for (int j = 0; j < i; j++)Line(pointstack[j], pointstack[j + 1]);
setlinecolor(WHITE);
Line(pointstack[i], pointstack[i + 1]);
}
else // 这个点属于凸包,让上一个点与这个点连红线
{
setlinecolor(RED);
AnimateLine(pointstack[i - 1], pointstack[i], 1);
DrawPointSet(pointstack);
for (int j = 0; j < i; j++)Line(pointstack[j], pointstack[j + 1]);
setlinecolor(WHITE);
Line(pointstack[i], pointstack[i + 1]);
parent = child;
}
if (i == pointstack.size() - 1) // i 是倒数第一个说明这个点是删除掉倒数第二个点后剩下的,只用画一条线
{
setlinecolor(RED);
AnimateLine(pointstack[pointstack.size() - 1], pointstack[0], 1);
DrawPointSet(pointstack);
for (int j = 0; j < pointstack.size() - 1; j++)Line(pointstack[j], pointstack[j + 1]);
}
else if (i == pointstack.size() - 2) // i 是倒数第二个说明倒数第二个点不用删除掉,所以要画两条线
{
setlinecolor(RED);
AnimateLine(pointstack[pointstack.size() - 1], pointstack[pointstack.size() - 2], 1);
AnimateLine(pointstack[pointstack.size() - 1], pointstack[0], 1);
DrawPointSet(pointstack);
for (int j = 0; j < pointstack.size(); j++)
Line(pointstack[j], pointstack[(j + 1) % pointstack.size()]);
}
}
return pointstack;
}
int main()
{
initgraph(WIDTH, HEIGHT);
setfillcolor(RED);
setlinestyle(PS_SOLID, 2);
ExMessage msg;
bool isExit = false;
bool isPressL = false, isPressR = false; // 避免能拖动增加点
vector<Point> pointset;
while (!isExit)
{
getmessage(&msg, EM_MOUSE | EM_KEY);
if (msg.message == WM_KEYDOWN)
{
switch (msg.vkcode)
{
case VK_RETURN:
isExit = true;
break;
case VK_SPACE:
pointset = ConvexHullAlgorithm(pointset);
break;
}
}
else
{
if (!isPressL && msg.lbutton)
{
isPressL = true;
if (!isInPointSet(pointset, msg.x, msg.y))
pointset.push_back({ (double)msg.x, (double)msg.y });
DrawPointSet(pointset);
}
else if (!isPressR && msg.rbutton)
{
if (isInPointSet(pointset, msg.x, msg.y))
{
for (std::vector<Point>::iterator ite = pointset.begin(); ite != pointset.end(); ite++)
{
if (GetLength(*ite, { (double)msg.x, (double)msg.y }) < RADIUS)
{
pointset.erase(ite);
break;
}
}
}
isPressR = true;
DrawPointSet(pointset);
}
else if (isPressL && !msg.lbutton)
{
isPressL = false;
}
else if (isPressR && !msg.rbutton)
{
isPressR = false;
}
}
}
return 0;
}

for (int i = 0; i < pointset.size(); i++)
{
if (i == index)continue;
pointstack.push_back(pointset[i]); // 将这个点放入点栈
double CosAngle = GetCosAngle(pointset[index], pointset[i]); // 求这个点与最左边的点的连线与基线的夹角
int temp = pointstack.size() - 1; // 得到点栈最后一个点也就是点集当前这个点
// 用插入排序将当前找到的点放入点栈
while (GetCosAngle(pointset[index], pointstack[temp - 1]) < CosAngle && temp > 1)
{
swap(pointstack, temp, temp - 1);
temp--;
}
}
可不可以优化掉{while循环每次调GetCosAngle}我的想法是把cosAngle值作为point的另外一个属性保存下来,这样就不需要每次从新去计算。