做一个旋转的立体几何，这个立体几何为三个相互嵌套着的正方体，让这三个大小不一的正方体分别绕着不同的轴线旋转。

1.初始时的就是一个正视图为正方形中心在原点的正方体，称之为初始状态。
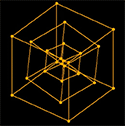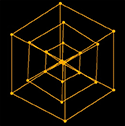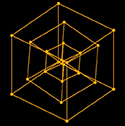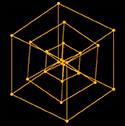
2.调整正方体使其两个顶点以及中心在 Z 轴上，此时正方体的正视图为正六边形，也就是展示状态。

3.在旋转的时候，需要将正方体调整回初始状态，旋转完毕后再调整为展示状态。

4.从三维直角坐标系中左手系的来说，最外围的正方体沿着 Y 轴转动，中间的正方体沿着 XOZ 平面中 x+z=0 轴线转动，最内的正方体沿着 XOZ 平面中 x-z=0 轴线转动。
这样的转动效果是三个正方体的六个顶点在中心位置不断交汇，立体几何不断旋转再生。

图片展示：

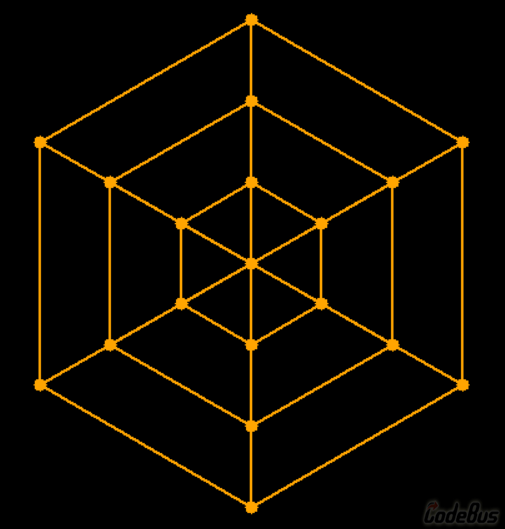
视频展示：

源码 :

////////////////////////////////////////
// 程序：无限循环几何
// 作者：肥美虎
// 编译环境：Visual C++ 6.0，EasyX_20210730
// 编写日期：2022-1-23

////////// 头文件 ////////////
#include<graphics.h>
#include<conio.h>
#include<math.h>

///////// 绘制的高度和宽度 /////////
#define Width 640
#define Height 480
#define N 8
const double PI = acos(-1.0);

// 记录三维点的坐标
struct point3d
{
	double x;
	double y;
	double z;
};
// 记录正交投影后绘图时的坐标
struct point2d
{
	int x;
	int y;
};

// 数据初始化，初始状态
void init_start(point3d Point1[N], point3d Point2[N], point3d Point3[N])
{
	Point1[0].x = -3; Point1[0].y = -3; Point1[0].z = -3;
	Point1[1].x = -3; Point1[1].y = -3; Point1[1].z = 3;
	Point1[2].x = -3; Point1[2].y = 3; Point1[2].z = 3;
	Point1[3].x = 3; Point1[3].y = 3; Point1[3].z = 3;
	Point1[4].x = 3; Point1[4].y = 3; Point1[4].z = -3;
	Point1[5].x = 3; Point1[5].y = -3; Point1[5].z = -3;
	Point1[6].x = -3; Point1[6].y = 3; Point1[6].z = -3;
	Point1[7].x = 3; Point1[7].y = -3; Point1[7].z = 3;
	Point2[0].x = -2; Point2[0].y = -2; Point2[0].z = -2;
	Point2[1].x = -2; Point2[1].y = -2; Point2[1].z = 2;
	Point2[2].x = -2; Point2[2].y = 2; Point2[2].z = 2;
	Point2[3].x = 2; Point2[3].y = 2; Point2[3].z = 2;
	Point2[4].x = 2; Point2[4].y = 2; Point2[4].z = -2;
	Point2[5].x = 2; Point2[5].y = -2; Point2[5].z = -2;
	Point2[6].x = -2; Point2[6].y = 2; Point2[6].z = -2;
	Point2[7].x = 2; Point2[7].y = -2; Point2[7].z = 2;
	Point3[0].x = -1; Point3[0].y = -1; Point3[0].z = -1;
	Point3[1].x = -1; Point3[1].y = -1; Point3[1].z = 1;
	Point3[2].x = -1; Point3[2].y = 1; Point3[2].z = 1;
	Point3[3].x = 1; Point3[3].y = 1; Point3[3].z = 1;
	Point3[4].x = 1; Point3[4].y = 1; Point3[4].z = -1;
	Point3[5].x = 1; Point3[5].y = -1; Point3[5].z = -1;
	Point3[6].x = -1; Point3[6].y = 1; Point3[6].z = -1;
	Point3[7].x = 1; Point3[7].y = -1; Point3[7].z = 1;
}

// 调整正方体的初始位置，让其两个端点在 Z 轴上，达到正视图为六边形的效果，调整后为展示状态
void adjust(point3d Point1[N], point3d Point2[N], point3d Point3[N])
{
	double x; int i;
	for (i = 0; i < N; i++)
	{
		x = Point1[i].x;
		Point1[i].x = cos(PI / 4) * Point1[i].x - Point1[i].z * sin(PI / 4);
		Point1[i].z = cos(PI / 4) * Point1[i].z + sin(PI / 4) * x;
	}
	for (i = 0; i < N; i++)
	{
		x = Point2[i].x;
		Point2[i].x = cos(PI / 4) * Point2[i].x - Point2[i].z * sin(PI / 4);
		Point2[i].z = sin(PI / 4) * x + cos(PI / 4) * Point2[i].z;
	}
	for (i = 0; i < N; i++)
	{
		x = Point3[i].x;
		Point3[i].x = cos(PI / 4) * Point3[i].x - Point3[i].z * sin(PI / 4);
		Point3[i].z = cos(PI / 4) * Point3[i].z + sin(PI / 4) * x;
	}
	for (i = 0; i < N; i++)
	{
		x = Point1[i].y;
		Point1[i].y = Point1[i].y * sqrt(6.0) / 3 - Point1[i].z * sqrt(3.0) / 3;
		Point1[i].z = x * sqrt(3.0) / 3 + Point1[i].z * sqrt(6.0) / 3;
	}
	for (i = 0; i < N; i++)
	{
		x = Point2[i].y;
		Point2[i].y = Point2[i].y * sqrt(6.0) / 3 - Point2[i].z * sqrt(3.0) / 3;
		Point2[i].z = x * sqrt(3.0) / 3 + Point2[i].z * sqrt(6.0) / 3;
	}
	for (i = 0; i < N; i++)
	{
		x = Point3[i].y;
		Point3[i].y = Point3[i].y * sqrt(6.0) / 3 - Point3[i].z * sqrt(3.0) / 3;
		Point3[i].z = x * sqrt(3.0) / 3 + Point3[i].z * sqrt(6.0) / 3;
	}
}

// 对三维正方体进行正交投影
point2d orthographic_Project(point3d p)
{
	point2d p2d;
	p2d.x = (int)(p.x * 40) + 320;
	p2d.y = (int)(p.y * 40) + 240;
	return p2d;
}

// 连接正方体顶点，绘制图形
void display(point2d p2d1[N], point2d p2d2[N], point2d p2d3[N])
{
	int i;
	for (i = 0; i < 5; i++)
	{
		line(p2d1[i].x, p2d1[i].y, p2d1[i + 1].x, p2d1[i + 1].y);
		line(p2d2[i].x, p2d2[i].y, p2d2[i + 1].x, p2d2[i + 1].y);
		line(p2d3[i].x, p2d3[i].y, p2d3[i + 1].x, p2d3[i + 1].y);
	}
	line(p2d1[5].x, p2d1[5].y, p2d1[0].x, p2d1[0].y);
	line(p2d2[5].x, p2d2[5].y, p2d2[0].x, p2d2[0].y);
	line(p2d3[5].x, p2d3[5].y, p2d3[0].x, p2d3[0].y);
	for (i = 0; i < 5; i = i + 2)
	{
		line(p2d1[6].x, p2d1[6].y, p2d1[i].x, p2d1[i].y);
		line(p2d2[6].x, p2d2[6].y, p2d2[i].x, p2d2[i].y);
		line(p2d3[6].x, p2d3[6].y, p2d3[i].x, p2d3[i].y);
	}
	for (i = 1; i < 6; i = i + 2)
	{
		line(p2d1[7].x, p2d1[7].y, p2d1[i].x, p2d1[i].y);
		line(p2d2[7].x, p2d2[7].y, p2d2[i].x, p2d2[i].y);
		line(p2d3[7].x, p2d3[7].y, p2d3[i].x, p2d3[i].y);
	}
}

// 最外围正方体的旋转，沿着 Y 轴
void Rotate1(point3d p3d[N], double angle)
{
	double x; int i;
	for (i = 0; i < N; i++) // 调整回初始状态
	{
		x = p3d[i].y;
		p3d[i].y = p3d[i].y * sqrt(6.0) / 3 + p3d[i].z * sqrt(3.0) / 3;
		p3d[i].z = -x * sqrt(3.0) / 3 + p3d[i].z * sqrt(6.0) / 3;
	}
	for (i = 0; i < N; i++)
	{
		x = p3d[i].x;
		p3d[i].x = p3d[i].x * cos(angle) + p3d[i].z * sin(-angle);
		p3d[i].z = x * sin(angle) + p3d[i].z * cos(angle);
	}
	for (i = 0; i < N; i++) // 调整回展示状态
	{
		x = p3d[i].y;
		p3d[i].y = p3d[i].y * sqrt(6.0) / 3 - p3d[i].z * sqrt(3.0) / 3;
		p3d[i].z = x * sqrt(3.0) / 3 + p3d[i].z * sqrt(6.0) / 3;
	}
}

// 中间正方体旋转，沿着 XOZ 平面的 x+y=0
void Rotate2(point3d p3d[N], double angle)
{
	double x; int i;
	for (i = 0; i < N; i++)
	{
		x = p3d[i].y;
		p3d[i].y = p3d[i].y * sqrt(6.0) / 3 + p3d[i].z * sqrt(3.0) / 3;
		p3d[i].z = -x * sqrt(3.0) / 3 + p3d[i].z * sqrt(6.0) / 3;
	}
	for (i = 0; i < N; i++) // 先旋转到 Z 轴，再绕 Z 轴旋转，接着旋转回来，就完成了绕 x+y=0 旋转
	{
		x = p3d[i].x;
		p3d[i].x = p3d[i].x * cos(PI / 4) - p3d[i].z * sin(PI / 4);
		p3d[i].z = x * sin(PI / 4) + p3d[i].z * cos(PI / 4);
	}
	for (i = 0; i < N; i++)
	{
		x = p3d[i].x;
		p3d[i].x = p3d[i].x * cos(angle) + p3d[i].y * sin(-angle);
		p3d[i].y = x * sin(angle) + p3d[i].y * cos(angle);
	}
	for (i = 0; i < N; i++)
	{
		x = p3d[i].x;
		p3d[i].x = p3d[i].x * cos(-PI / 4) - p3d[i].z * sin(-PI / 4);
		p3d[i].z = x * sin(-PI / 4) + p3d[i].z * cos(-PI / 4);
	}
	for (i = 0; i < N; i++)
	{
		x = p3d[i].y;
		p3d[i].y = p3d[i].y * sqrt(6.0) / 3 - p3d[i].z * sqrt(3.0) / 3;
		p3d[i].z = x * sqrt(3.0) / 3 + p3d[i].z * sqrt(6.0) / 3;
	}
}

// 最内层正方体旋转，沿着 XOY 平面的 x=y
void Rotate3(point3d p3d[N], double angle)
{
	double x; int i;
	for (i = 0; i < N; i++)
	{
		x = p3d[i].y;
		p3d[i].y = p3d[i].y * sqrt(6.0) / 3 + p3d[i].z * sqrt(3.0) / 3;
		p3d[i].z = -x * sqrt(3.0) / 3 + p3d[i].z * sqrt(6.0) / 3;
	}
	for (i = 0; i < N; i++)
	{
		x = p3d[i].x;
		p3d[i].x = p3d[i].x * cos(-PI / 4) - p3d[i].z * sin(-PI / 4);
		p3d[i].z = x * sin(-PI / 4) + p3d[i].z * cos(-PI / 4);
	}
	for (i = 0; i < N; i++)
	{
		x = p3d[i].x;
		p3d[i].x = p3d[i].x * cos(angle) + p3d[i].y * sin(-angle);
		p3d[i].y = x * sin(angle) + p3d[i].y * cos(angle);
	}
	for (i = 0; i < N; i++)
	{
		x = p3d[i].x;
		p3d[i].x = p3d[i].x * cos(PI / 4) - p3d[i].z * sin(PI / 4);
		p3d[i].z = x * sin(PI / 4) + p3d[i].z * cos(PI / 4);
	}
	for (i = 0; i < N; i++)
	{
		x = p3d[i].y;
		p3d[i].y = p3d[i].y * sqrt(6.0) / 3 - p3d[i].z * sqrt(3.0) / 3;
		p3d[i].z = x * sqrt(3.0) / 3 + p3d[i].z * sqrt(6.0) / 3;
	}
}
int main()
{
	initgraph(Width, Height);
	setlinecolor(RGB(255, 165, 0)); // 设置颜色
	setfillcolor(RGB(255, 165, 0));
	setlinestyle(PS_SOLID, 2); // 加粗连接线条
	point3d Point1[N];
	point3d Point2[N];
	point3d Point3[N];
	point2d p2d1[N];
	point2d p2d2[N];
	point2d p2d3[N];
	init_start(Point1, Point2, Point3); // 初始化数据
	adjust(Point1, Point2, Point3); // 调整数据
	BeginBatchDraw();
	while (true)
	{
		for (int i = 0; i < N; i++)
		{
			p2d1[i] = orthographic_Project(Point1[i]); // 投影
			p2d2[i] = orthographic_Project(Point2[i]);
			p2d3[i] = orthographic_Project(Point3[i]);
			solidcircle((int)p2d1[i].x, (int)p2d1[i].y, 5); // 绘制顶点
			solidcircle((int)p2d2[i].x, (int)p2d2[i].y, 5);
			solidcircle((int)p2d3[i].x, (int)p2d3[i].y, 5);
		}
		display(p2d1, p2d2, p2d3); // 连接
		Sleep(20);
		Rotate1(Point1, PI / 180); // 旋转
		Rotate2(Point2, PI / 180);
		Rotate3(Point3, PI / 180);
		FlushBatchDraw();

		cleardevice();
	}
	EndBatchDraw();
	_getch();
	closegraph();
	return 0;
}