LOVE MY D.O.

分形几何学是一门以不规则几何形态为研究对象的几何学。一个数学意义上分形的生成是基于一个不断迭代的方程式，即一种基于递归的反馈系统。虽然分形是一个数学构造，它们同样可以在自然界中被找到，这使得它们被划入艺术作品的范畴。

计算机协助了人们推开分形几何的大门。法国数学家曼德尔勃罗特这位计算机和数学兼通的人物，开创了新的数学分支——分形几何学。分形在医学、土力学、地震学和技术分析中都有应用。

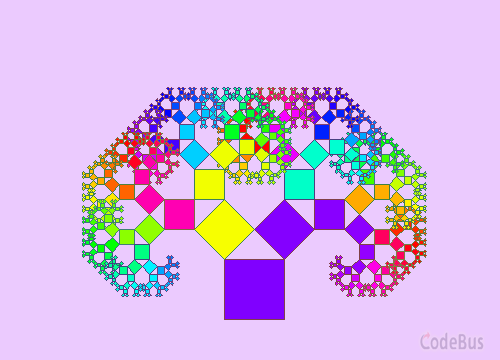
毕达哥拉斯树（Pythagoras tree）是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的图形。又因为重复数次后的形状好似一棵树，所以被称为毕达哥拉斯树，也叫“勾股树”。

这个程序，展示了毕达哥拉斯树的生成。执行效果如下：

我的求解思路是：

1. 确定直线 p1-p2，并在 p1-p2 的左侧求出 p11-p22，使 p1-p2-p22-p11 构成正方形。
2. 求出点 p，使  p-p11-p22 构成含 60 度角的直角三角形。
3. 分别将直线 p-p11 和 p-p22 看作 p1-p2，递归。递归的条件是正方形的边长大于 3。

完成的 C 语言源代码如下：

///////////////////////////////////////////////////
// 程序名称：毕达哥拉斯树（Pythagoras tree）
// 编译环境：Mictosoft Visual Studio 2010, EasyX_20200315(beta)
// 作　　者：LOVE MY D.O. <1509840721@qq.com>
// 最后修改：2020-4-10
//
#include <graphics.h>
#include <conio.h>
#include <math.h>

const double PI = 3.1415926536;

// 定义一个结构体 Point，存储点的坐标
struct Point
{
	double x;
	double y;
};

// 直线的旋转（p1 是定点）
Point Rotate(Point p1, Point p2, double angle)
{
	Point r;
	r.x = p1.x + (p2.x - p1.x) * cos(angle) + (p2.y - p1.y) * sin(angle);
	r.y = p1.y + (p2.y - p1.y) * cos(angle) - (p2.x - p1.x) * sin(angle);
	return r;
}

// 直线的缩放（p1 是定点）
Point Zoom(Point p1, Point p2, double ratio)
{
	Point r;
	r.x = p1.x + (p2.x - p1.x) * ratio;
	r.y = p1.y + (p2.y - p1.y) * ratio;
	return r;
}

// 画出正方形
void Draw(Point p1, Point p2)
{
	Point p11 = Rotate(p1, p2, 90 * PI / 180);
	Point p22 = Rotate(p2, p1, 270 * PI / 180);

	POINT pts[] = { { int(p1.x + 0.5),  int(p1.y + 0.5) },					// +0.5 是为了四舍五入
					{ int(p2.x + 0.5),  int(p2.y + 0.5) },
					{ int(p22.x + 0.5), int(p22.y + 0.5) }, 
					{ int(p11.x + 0.5), int(p11.y + 0.5) } };

	static int color_H = 270;
	setfillcolor(HSVtoRGB(float(color_H), 1, 1));							// 设置正方形的填充颜色
	setlinecolor(HSVtoRGB(float((color_H + 80) % 360), 0.5, 0.5));			// 设置正方形的边框颜色
	color_H = (color_H + 1) % 360;
	fillpolygon(pts, 4);													// 填充正方形颜色

	if (((p22.x - p11.x) * (p22.x - p11.x) + (p22.y - p11.y) * (p22.y - p11.y)) > 3 * 3 )	// 正方形的边长 >3 时递归
	{
		double a = 60 * PI / 180;					// 60 度形式
//		double a = 45 * PI / 180;					// 45 度形式
		Point p = Rotate(p11, p22, a);
		p = Zoom(p11, p, cos(a));

		Draw(p, p22);
		Draw(p11, p);
	}
}

// 主函数
int main()
{
	initgraph(640, 480);				// 初始化窗口
	setbkcolor(0xfecaeb);				// 设置背景颜色
	cleardevice();

	Point p1 = { 290, 400 };
	Point p2 = { 350, 400 };
	Draw(p1, p2);

	_getch();
	closegraph();						// 关闭窗口
	return 0;
}

其中，改变旋转的角度可以产生不同形状的树。例如，修改 Draw 函数里的 double a 变量为 45 度，可以得到这样的效果：