游戏中二维碰撞反弹算法分析与实现

前言
这篇文章主要是来分析一下在游戏中,如何处理二维碰撞问题(主要是圆和矩形的碰撞问题),以及如何处理在实际项目遇到的一些问题。
这篇文章虽然只以圆和矩形的碰撞问题举例分析,但是很多其他碰撞问题的处理方法都是类似的,所以也可以将本文所述的算法应用到其他情况下。
本文的末尾会给出完整可编译的示例代码,这里先放个效果图:

为什么写这篇文章呢?因为我最近做了个游戏:BricksBeater,其中最重要的问题就是处理运动的圆与固定矩形的碰撞。但是网上搜到的处理碰撞反弹的文章大多不尽人意,例如:
这一篇文章写得很好,但考虑的仍然不全面。我们知道圆与矩形碰撞可以这样分为三种情况:

前两种情况很容易考虑到,也比较好处理,但是很少有人提及第三种情况。所以,我写了本文,重新来分析一下圆和矩形的碰撞问题,并重点分析第三种情况。
附 BricksBeater 游戏项目链接:
CodeBus: https://codebus.cn/huidong/bricks-beater
Github: https://github.com/zouhuidong/BricksBeater
背景设定
在游戏中常常需要处理类似下面的碰撞问题:
- 打篮球游戏,篮球与水平地面的碰撞(动圆与固定直线碰撞)
- 打台球游戏,动圆碰撞动圆(还有动圆碰撞固定的圆)
- 运动的圆与墙壁碰撞(动圆和固定矩形的碰撞)
- 运动的圆与运动的矩形碰撞
- 矩形之间的碰撞
- ……
总的来说,从碰撞双方的运动性质上可以分为两类:
- 动的打动的(运动的物体碰撞可以运动的物体,后者可以没有初速度)
- 动的打不动的(运动的物体碰撞不能运动的物体,比如和墙碰撞)
从碰撞双方的接触关系上可以分为三类:
- 点与点的碰撞
- 点与线的碰撞
- 线与线的碰撞
这里只考虑二维碰撞,那么,圆与矩形碰撞就是点与线碰撞或点与点碰撞、圆与圆碰撞就是点与点碰撞,此外还有矩形相撞,即线与线碰撞。
本文专门来讨论一下,“动的打不动的”问题中的“点与点的碰撞”和“点与线的碰撞”,并以动圆碰撞固定矩形(未旋转的)举例来分析,对于其它类似碰撞问题,处理方式也是大同小异。
注:如果你想解决“动的打动的”问题,这需要动量守恒定律的知识,可以看看这篇文章,本文不详细讨论;关于与旋转的矩形碰撞的问题,其实可以以矩形的相邻两边重新建立坐标系,就又变成未旋转的矩形了,可以参考这篇文章,本文也不详细讨论。
理论分析
我们先从一个动圆碰撞一个固定矩形分析,那么就会有三种情况:

对应第一种情况,我们只需要把小球的 x 方向的速度乘以 -1 即可,同理,对于第二种情况,只需要将 y 方向的速度乘以 -1 即可。
对于第三种情况,显然不能看作前两种情况的组合,如果这样的话,小球碰到顶点后,速度直接反向了,很容易看出这是不可能的。
第三种情况的正确处理方式:首先连接发生碰撞的矩形顶点和小球圆心,如下图,使得∠A = ∠B。
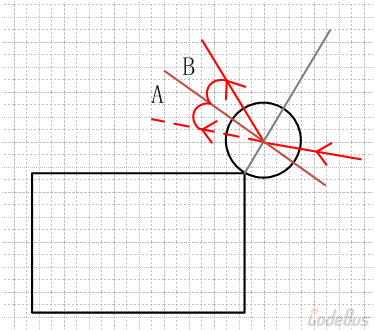
设入射角为α,反射角为β,顶点和小球圆心所在直线的倾斜角为(θ – 90°),那么,就可以像这样建立坐标系:
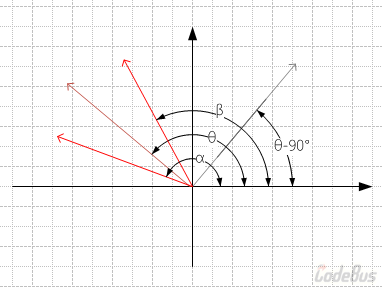
易知:
α - θ = θ – β
即:
β = 2θ – α
由此,我们就可以根据 β 求出反射速度的水平和竖直分量了。
程序中的处理
虽然理论上分析很简单,但是在程序中,小球的运动是离散的而非连续的,所以需要处理更多的问题。本节来处理这些问题。
由于在游戏中通常都不会只存在一个矩形会与小球碰撞,所以我们假设有多个矩形,所有的矩形都位于网格地图中整齐地排布,像这样:

碰撞检测
处理反弹首先要检测碰撞。由于我们已经假设地图是网格状的,所以我们可以让小球与以它为中心的一个九宫格内的所有矩形进行碰撞检测。
因为程序中存储的小球坐标 x 和 y 会在每一次游戏循环(每一帧)中分别加等于 x 和 y 速度分量,所以小球的运动并不连续。这就会导致判定小球碰撞时,小球已经和矩形发生重叠了,如下图:
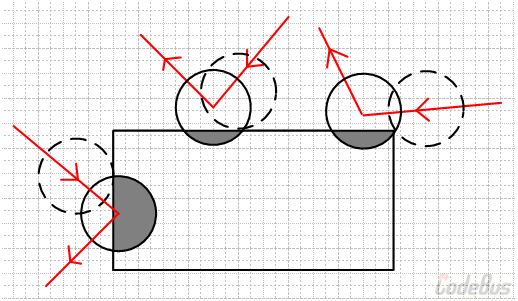
所以我们检测碰撞时,可以找出待检测矩形中距离圆心最近的一点,并判断它们的距离是否小于半径。找出最近点的过程可以拆分为 x 和 y 两个方向。也就是先在矩形内部,找出一个 x 坐标,使其与圆心的 x 坐标的距离最小,然后对于 y 坐标重复这个操作。这样,我们就得到了矩形中离圆心最近的一点。如下代码:
// 获取点到矩形的最小距离
float GetDistance_PointToRect(float x, float y, RECT rct)
{
float x_rct, y_rct; // 保存矩形内到目标点最近的点
if (x >= rct.left && x <= rct.right)
x_rct = x;
else
x_rct = (float)(fabsf(x - rct.left) < fabsf(x - rct.right) ? rct.left : rct.right);
if (y >= rct.top && y <= rct.bottom)
y_rct = y;
else
y_rct = (float)(fabsf(y - rct.top) < fabsf(y - rct.bottom) ? rct.top : rct.bottom);
float dx = x - x_rct;
float dy = y - y_rct;
return sqrtf(dx * dx + dy * dy);
}
如果圆半径比较小,那么也可以直接粗略判定:直接取圆的上下左右四个顶点,判断其是否位于矩形区域内,如果是,则判定碰撞。
反弹处理
首先,我们应该先判定小球是不是和矩形的顶点发生碰撞,我们暂且称其为“顶点碰撞”。
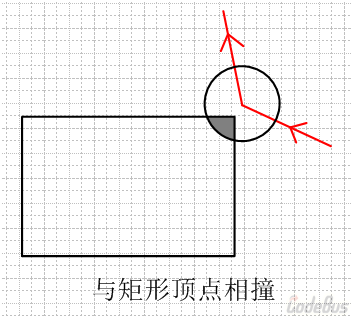
判定顶点碰撞无需将四个顶点逐个尝试,应该采取如下步骤:
- 如果小球同时跨越了矩形的两条边界,那么就可以直接确定,只有这两条边界的公共顶点有可能发生顶点碰撞。
- 如果小球只跨越了一条边界,那么我们可以认为这条边界所对应的两个顶点中,距离圆心更近的一个顶点才有可能发生顶点碰撞。
这样我们就选定好了“潜力顶点”,知道了哪个顶点可能发生“顶点碰撞”。
如果这的确是个“顶点碰撞”,那么因为小球的运动是离散的,所以一般这个时候已经小球已经超过了和顶点碰撞的位置(也就是相切的位置),因此接下来,我们要计算出小球与顶点相切时的位置,以便计算反射方向。
我们可以根据小球的速度和当前坐标,反推出上一帧的小球坐标。这样,我们就可以根据这两个坐标描述小球的运动轨迹直线(记为直线 l,下图红色虚线)。然后,我们还可以描述出以“潜力顶点”为圆心,半径等于小球半径的圆的方程(记为圆 O,下图绿圆)。
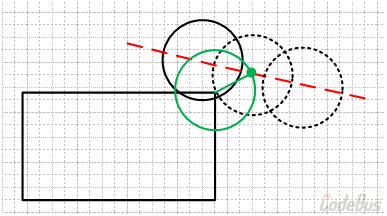
只要联立直线 l 和 圆 O,就会得到一个二次方程,如果方程有解,就可以求出小球与顶点相切时的坐标了(一般会解得两个解,取靠近上一帧圆心坐标的解),若无解就说明不发生顶点碰撞。这只需要中学数学知识,故此处省略数学过程,后面会给出函数。
但是,到这一步还不能确定一定发生顶点碰撞,因为也有可能是下图的情况,虽然也解得了相切坐标,但是这个圆仍然和矩形重叠,是不存在的情况。
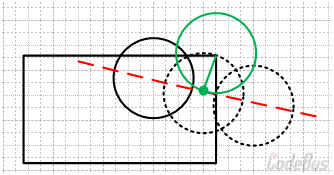
所以解得相切坐标后,还需要求此坐标到矩形的最小距离(上一节已讲求解方法),只要解得的距离小于半径,那么就说明这是“假碰撞”,又名“碰瓷”,不算顶点碰撞。
经过上述步骤,就可以确定此次碰撞是不是顶点碰撞了。下面给出求解相切坐标的函数:
// 根据圆的轨迹直线,获取圆与某点相切时的圆心坐标
// 返回是否存在相切
bool GetTangentCirclePoint(
float x0, // 切点坐标
float y0,
float x1, // 圆心轨迹直线上的一点(更早运动到的点)
float y1,
float x2, // 圆心轨迹直线上的另一点(其实运动不到的点)
float y2,
float r, // 圆半径
float* p_out_x, // 输出圆心坐标
float* p_out_y
)
{
// 斜率不存在时
if (fabsf(x1 - x2) < 0.00001f)
{
// 计算相切时圆心与切点的竖直距离
float d2 = r * r - (x0 - x1) * (x0 - x1);
if (d2 < 0)
return false;
float d = sqrtf(d2);
// 求出两组解
float _y1 = y0 + d;
float _y2 = y0 - d;
// 保留离 (x1, y1) 更近的解
float _y_closer = fabsf(y1 - _y1) < fabsf(y1 - _y2) ? _y1 : _y2;
*p_out_x = x1;
*p_out_y = _y_closer;
return true;
}
// 圆心轨迹直线方程:y - y1 = (y2 - y1) / (x2 - x1) * (x - x1)
// 即:y = kx - kx1 + y1
// 圆的方程:(x - x0) ^ 2 + (y - y0) ^ 2 = r ^ 2
// 联立得二次函数,如下。
float k = (y2 - y1) / (x2 - x1); // 直线斜率
float m = -k * x1 + y1 - y0; // 部分常数
float a = k * k + 1; // 二次函数的 abc 系数
float b = 2 * (k * m - x0);
float c = x0 * x0 + m * m - r * r;
float delta = b * b - 4 * a * c; // 判别式
if (delta < 0) // 无解
return false;
float sqrt_delta = sqrtf(delta); // 判别式开根号
float _x1 = (-b + sqrt_delta) / (2 * a); // 两个根
float _x2 = (-b - sqrt_delta) / (2 * a);
// 保留离 (x1, y1) 更近的解
float _x_closer = fabsf(x1 - _x1) < fabsf(x1 - _x2) ? _x1 : _x2;
float _y = k * _x_closer - k * x1 + y1;
*p_out_x = _x_closer;
*p_out_y = _y;
return true;
}
再次提醒,调用上面的函数求得相切时的圆心坐标后,还需要判断“碰瓷”行为。
最后,在确定顶点碰撞后,就使用我们在理论分析时推导出来的公式计算反射角度即可,公式如下:
β = 2θ – α
下面给出处理顶点碰撞的代码,注意,下面的代码中调用的函数都是上文已经给出的。
// 碰撞时的小球圆心坐标(即与顶点相切时的坐标)
float fCollisionX, fCollisionY;
if (!GetTangentCirclePoint( // 获取相切时的圆心坐标
fVertex_X, // 顶点坐标(前面已经求出)
fVertex_Y,
last_x, // 上一帧的圆心坐标
last_y,
ball->x, // 当前圆心坐标
ball->y,
(float)g_nBallRadius, // 小球半径
&fCollisionX, // 传入指针
&fCollisionY
))
{
// 没有相切,说明顶点碰撞不成立
//
// TODO ...
return;
}
// 如果是真的相切,则相切时矩形到圆心的最近距离应该等于小球半径
// 但如果此时小于半径,那么说明是假相切
if (GetDistance_PointToRect(fCollisionX, fCollisionY, rct) < g_nBallRadius * 0.98f /* 允许一点误差 */)
{
// 顶点碰撞不成立
//
// TODO ...
return;
}
// 计算碰撞时,小球圆心到碰撞点(顶点)的坐标差
float f_dx = fCollisionX - fVertex_X;
float f_dy = fCollisionY - fVertex_Y;
// 求反射面弧度
float f_radianReflectingSurface = atan2f(f_dy, f_dx);
// 求法线弧度
float f_radianNormal = f_radianReflectingSurface + PI / 2 /* 或 - PI / 2 */;
// 求小球入射弧度
float f_radianIncidence = atan2f(ball->vy, ball->vx);
// 将小球速度沿法线对称,求得新的速度弧度
float f_radianReflection = 2 * f_radianNormal - f_radianIncidence;
// 求反射速度
ball->vx = cosf(f_radianReflection) * BALL_SPEED;
ball->vy = sinf(f_radianReflection) * BALL_SPEED;
最后还有一点要注意,因为此时判定到碰撞的时候,说明小球已经和矩形有重叠了,所以应该把小球坐标修正到相切时的小球坐标,如下:
// 修正小球坐标到相切时的坐标
ball->x = fCollisionX;
ball->y = fCollisionY;
至此,顶点碰撞的情况就处理完了。剩下的两种情况,也就是和矩形的竖直面或水平面碰撞的情况,都统称为普通碰撞吧。
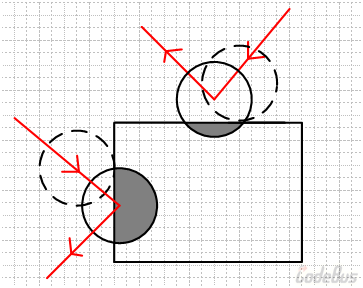
对于普通碰撞情况:如果小球和矩形左右边界相交,那么小球的 x 方向速度分量要翻转;如果与上下边界相交,那么 y 方向速度分量要翻转。
像顶点碰撞一样,最后也应该要修正小球坐标到相碰时的小球坐标。由于这只是几何计算问题,所以此处就略过了。也可以粗略地修正小球坐标为上一帧的坐标,但是注意:最好不要粗暴地修正为两帧的中点,因为小球在两帧中点时也有可能和矩形有重叠,从而导致再次判定碰撞,这样就有可能使小球陷入矩形内部。
特殊情况处理
现在已经基本处理完了碰撞问题,但是还需要解决一些实际应用中会出现的问题。
前面我们已经设定,游戏中存在有多个矩形,所有的矩形都位于网格地图中整齐地排布。如果小球与多个矩形碰撞,还会出现新的问题。
问题 1:周围矩形的碰撞干扰

如上图,当我们对小球和右边的矩形进行碰撞判定时,会发现小球跨越了右侧矩形的左边界和上边界,所以最后会判定为小球与右侧矩形的左上顶点发生顶点碰撞。但其实是错误的,因为左侧还有一个矩形存在,因此小球只能判定为与矩形上表面碰撞。
解决方案:对于连接着其它矩形的边界,即使小球跨越了它,也不能作为碰撞依据。
问题 2:陷入多个矩形内部的小球发生“漂移”(或陷入单个矩形内部的小球无限反弹)
有的时候,小球可能速度过快,前一帧还没有与矩形重叠,后一帧直接就进入矩形内部了,如下图:
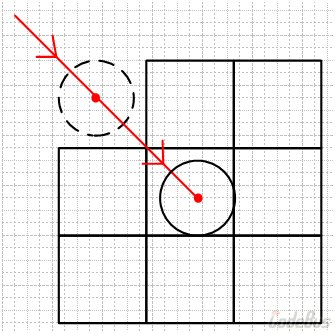
如果此时上面所说的问题 1 已经修复,那么小球在继续向右下方移动,并越过矩形边界的时候,由于小球处于多个紧挨着的矩形内部,所以每次跨越矩形边界都不能作为碰撞依据,这就会导致小球在矩形群落内部肆无忌惮地“穿墙”。
还有一种可能,小球进入了单个的矩形内部,那么由于矩形周围无物体,所以小球一旦跨越矩形的边界就可以作为碰撞依据,这就很可能导致小球在这个矩形内部无限反弹,如下图:
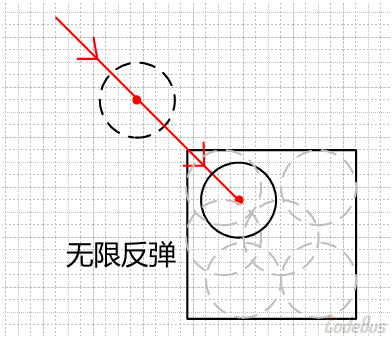
解决方案:可以每次处理小球碰撞时,判断圆心是否已经位于矩形内部,如果是,那么就直接设置小球回到上一帧的位置(因为上一帧一般不在矩形内),并使其速度反向,同时对速度加上不是很大的随机数(防止小球在两个地方持续反弹)。
但是,有时可能因为某些不确定的原因(例如误差积累等等原因),小球的上一帧坐标也在矩形内部,这种情况确实存在!如果不处理这种情况,小球就很可能出现卡墙、无限反弹等情况。
所以,我们还应该判断上一帧坐标是否也在矩形内部,如果是,那么就需要强制将小球移出矩形。此时我们可以判断小球跨越了矩形的哪条边界,就把小球从哪个方向移出去,比如跨越左边界,就把小球的 x 坐标设置为左边界的 x 坐标减去小球半径,其余边界以此类推,贴个代码:
// 得到小球上一帧的坐标
float last_x = (ball->x - ball->vx);
float last_y = (ball->y - ball->vy);
// 如果小球不慎进入砖块内部,此时应该回到上一帧,并使速度反向(同时加以扰动)
if (ball->x >= rct.left && ball->x <= rct.right
&& ball->y >= rct.top && ball->y <= rct.bottom)
{
ball->x = last_x;
ball->y = last_y;
// 如果上一帧仍然陷在里面
if (ball->x >= rct.left && ball->x <= rct.right
&& ball->y >= rct.top && ball->y <= rct.bottom)
{
// 强制弹出小球
if (ball->vx > 0 && left /* 左边界不与其他矩形相连 */) // 小球穿越左边界
{
ball->x = (float)(rct.left - g_nBallRadius);
}
else if (ball->vx < 0 && right /* 右边界不与其他矩形相连 */) // 小球穿越右边界
{
ball->x = (float)(rct.right + g_nBallRadius);
}
if (ball->vy > 0 && up /* 上边界不与其他矩形相连 */) // 小球穿越上边界
{
ball->y = (float)(rct.top - g_nBallRadius);
}
else if (ball->vy < 0 && down /* 下边界不与其他矩形相连 */) // 小球穿越下边界
{
ball->y = (float)(rct.bottom + g_nBallRadius);
}
}
ball->vx *= -1 + rand() % 10 / 1000.f;
ball->vy *= -1 + rand() % 10 / 1000.f;
}
此方案理论上可以解决大部分陷入问题。
示例代码
下面给出一个简单的示例,只演示了各个矩形独立存在(不会连在一起)的情况,如果想参考更完整的碰撞处理代码,请查阅 BricksBeater 项目源码。
注:这里再次给出 BricksBeater 游戏项目链接:
CodeBus: https://codebus.cn/huidong/bricks-beater
Github: https://github.com/zouhuidong/BricksBeater
上源码前先看看效果图:

上源码:
#include <graphics.h>
#include <math.h>
#include <time.h>
// 圆周率
#define PI 3.1415926f
// 窗口大小
#define WIDTH 640
#define HEIGHT 480
// 小球半径
#define RADIUS 20
// 小球速度
#define SPEED 10.f
// 小球
struct Ball
{
float x;
float y;
float vx;
float vy;
}ball;
// 获取点到矩形的最小距离
float GetDistance_PointToRect(float x, float y, RECT rct)
{
float x_rct, y_rct; // 保存矩形内到目标点最近的点
if (x >= rct.left && x <= rct.right)
x_rct = x;
else
x_rct = (float)(fabsf(x - rct.left) < fabsf(x - rct.right) ? rct.left : rct.right);
if (y >= rct.top && y <= rct.bottom)
y_rct = y;
else
y_rct = (float)(fabsf(y - rct.top) < fabsf(y - rct.bottom) ? rct.top : rct.bottom);
float dx = x - x_rct;
float dy = y - y_rct;
return sqrtf(dx * dx + dy * dy);
}
// 根据圆的轨迹直线,获取圆与某点相切时的圆心坐标
// 返回是否存在相切
bool GetTangentCirclePoint(
float x0, // 切点坐标
float y0,
float x1, // 圆心轨迹直线上的一点(更早运动到的点)
float y1,
float x2, // 圆心轨迹直线上的另一点(其实运动不到的点)
float y2,
float r, // 圆半径
float* p_out_x, // 输出圆心坐标
float* p_out_y
)
{
// 斜率不存在时
if (fabsf(x1 - x2) < 0.00001f)
{
// 计算相切时圆心与切点的竖直距离
float d2 = r * r - (x0 - x1) * (x0 - x1);
if (d2 < 0)
return false;
float d = sqrtf(d2);
// 求出两组解
float _y1 = y0 + d;
float _y2 = y0 - d;
// 保留离 (x1, y1) 更近的解
float _y_closer = fabsf(y1 - _y1) < fabsf(y1 - _y2) ? _y1 : _y2;
*p_out_x = x1;
*p_out_y = _y_closer;
return true;
}
// 圆心轨迹直线方程:y - y1 = (y2 - y1) / (x2 - x1) * (x - x1)
// 即:y = kx - kx1 + y1
// 圆的方程:(x - x0) ^ 2 + (y - y0) ^ 2 = r ^ 2
// 联立得二次函数,如下。
float k = (y2 - y1) / (x2 - x1); // 直线斜率
float m = -k * x1 + y1 - y0; // 部分常数
float a = k * k + 1; // 二次函数的 abc 系数
float b = 2 * (k * m - x0);
float c = x0 * x0 + m * m - r * r;
float delta = b * b - 4 * a * c; // 判别式
if (delta < 0) // 无解
return false;
float sqrt_delta = sqrtf(delta); // 判别式开根号
float _x1 = (-b + sqrt_delta) / (2 * a); // 两个根
float _x2 = (-b - sqrt_delta) / (2 * a);
// 保留离 (x1, y1) 更近的解
float _x_closer = fabsf(x1 - _x1) < fabsf(x1 - _x2) ? _x1 : _x2;
float _y = k * _x_closer - k * x1 + y1;
*p_out_x = _x_closer;
*p_out_y = _y;
return true;
}
// 小球碰撞处理
// rct 碰撞箱区域
//
// 返回是否发生碰撞
bool BallCollisionProcess(RECT rct)
{
// 得到小球上一帧的坐标
float last_x = (ball.x - ball.vx);
float last_y = (ball.y - ball.vy);
bool is_collision = false; // 是否发生碰撞
// 如果小球不慎进入砖块内部,此时应该回到上一帧,并使速度反向(同时加以扰动)
if (ball.x >= rct.left && ball.x <= rct.right
&& ball.y >= rct.top && ball.y <= rct.bottom)
{
ball.x = last_x;
ball.y = last_y;
// 如果上一帧仍然陷在里面
if (ball.x >= rct.left && ball.x <= rct.right
&& ball.y >= rct.top && ball.y <= rct.bottom)
{
// 强制弹出小球
if (ball.vx > 0)
{
ball.x = (float)(rct.left - RADIUS);
}
else if (ball.vx < 0)
{
ball.x = (float)(rct.right + RADIUS);
}
if (ball.vy > 0)
{
ball.y = (float)(rct.top - RADIUS);
}
else if (ball.vy < 0)
{
ball.y = (float)(rct.bottom + RADIUS);
}
}
ball.vx *= -1 + rand() % 10 / 100.f;
ball.vy *= -1 + rand() % 10 / 100.f;
return true;
}
// 首先需要保证矩形和圆有重叠
if (!(GetDistance_PointToRect(ball.x, ball.y, rct) <= RADIUS * 0.98f))
{
return false;
}
// 穿越碰撞箱边界标记
bool cross_left =
rct.left > ball.x
&& fabsf(ball.x - rct.left) <= RADIUS;
bool cross_right =
ball.x > rct.right
&& fabsf(ball.x - rct.right) <= RADIUS;
bool cross_top =
rct.top > ball.y
&& fabsf(ball.y - rct.top) <= RADIUS;
bool cross_bottom =
ball.y > rct.bottom
&& fabsf(ball.y - rct.bottom) <= RADIUS;
// 标记是否需要判断顶点碰撞
bool vertex_judge_flag = true;
float fVertex_X = 0; // 判定顶点碰撞时使用的顶点
float fVertex_Y = 0;
if (cross_left && cross_top) // 左上角
{
//vertex_judge_flag = true;
fVertex_X = (float)rct.left;
fVertex_Y = (float)rct.top;
}
else if (cross_right && cross_top) // 右上角
{
//vertex_judge_flag = true;
fVertex_X = (float)rct.right;
fVertex_Y = (float)rct.top;
}
else if (cross_left && cross_bottom) // 左下角
{
//vertex_judge_flag = true;
fVertex_X = (float)rct.left;
fVertex_Y = (float)rct.bottom;
}
else if (cross_right && cross_bottom) // 右下角
{
//vertex_judge_flag = true;
fVertex_X = (float)rct.right;
fVertex_Y = (float)rct.bottom;
}
// 如果没有同时穿越 xy 两个方向,就需要再评估用哪个顶点
else
{
// 如果穿越上下边界,则就只需要决定使用左边还是右边的顶点
if (cross_top || cross_bottom)
{
fVertex_Y = cross_top ? (float)rct.top : (float)rct.bottom; // 首先就可以确定 Y
fVertex_X =
(fabsf(ball.x - rct.left) < fabsf(ball.x - rct.right)) ?
(float)rct.left : (float)rct.right;
}
// 如果穿越左右边界
else if (cross_left || cross_right)
{
fVertex_X = cross_left ? (float)rct.left : (float)rct.right;
fVertex_Y =
(fabsf(ball.y - rct.top) < fabsf(ball.y - rct.bottom)) ?
(float)rct.top : (float)rct.bottom;
}
else
{
vertex_judge_flag = false;
}
}
// 优先判断是不是顶点碰撞
bool isVertexCollision = false; // 标记是否发生顶点碰撞
if (vertex_judge_flag) // 处理顶点碰撞问题
{
// 获取碰撞时的小球圆心坐标(即与顶点相切时的坐标)
float fCollisionX, fCollisionY;
if (!GetTangentCirclePoint(
fVertex_X,
fVertex_Y,
last_x,
last_y,
ball.x,
ball.y,
(float)RADIUS,
&fCollisionX,
&fCollisionY
))
{
// 没有相切,说明顶点碰撞不成立
goto tag_after_vertex_colision;
}
// 如果是真的相切,则相切时矩形到圆心的最近距离应该等于小球半径
// 但如果此时小于半径,那么说明是假相切
if (GetDistance_PointToRect(fCollisionX, fCollisionY, rct) < RADIUS * 0.98f /* 允许一点误差 */)
{
goto tag_after_vertex_colision;
}
// 计算碰撞时,小球圆心到碰撞点的坐标差
float f_dx = fCollisionX - fVertex_X;
float f_dy = fCollisionY - fVertex_Y;
// 求反射面弧度
float f_radianReflectingSurface = atan2f(f_dy, f_dx);
// 求法线弧度
float f_radianNormal = f_radianReflectingSurface + PI / 2 /* 或 - PI / 2 */;
// 求小球入射弧度
float f_radianIncidence = atan2f(ball.vy, ball.vx);
// 将小球速度沿法线对称,求得新的速度弧度
float f_radianReflection = 2 * f_radianNormal - f_radianIncidence;
// 求速度
ball.vx = cosf(f_radianReflection) * SPEED;
ball.vy = sinf(f_radianReflection) * SPEED;
// 修正小球坐标到相切时的坐标
ball.x = fCollisionX;
ball.y = fCollisionY;
isVertexCollision = true; // 标记发生顶点碰撞
is_collision = true;
}
tag_after_vertex_colision:
// 普通碰撞
if (!isVertexCollision)
{
// 跨越碰撞箱左右边界,则水平速度反转
if (cross_left || cross_right)
{
ball.vx = -ball.vx;
is_collision = true;
}
// 跨越碰撞箱上下边界,则竖直速度反转
if (cross_top || cross_bottom)
{
ball.vy = -ball.vy;
is_collision = true;
}
}
// 回溯坐标,即发生碰撞后,把小球从墙里“拔”出来(回到上一帧的位置),避免穿墙效果
// 如果发生的是顶点碰撞,那么在前面就已经进行了相切位置修正,就不需要回溯坐标了
if (!isVertexCollision && is_collision)
{
ball.x = last_x;
ball.y = last_y;
}
return is_collision;
}// BallCollisionProcess
// 绘制场景
// p_rct 矩形数组
// count 有几个矩形
// collision 小球是否发生了碰撞
void Render(RECT* p_rct, int count, bool collision)
{
setfillcolor(WHITE);
for (int i = 0; i < count; i++)
solidrectangle(p_rct[i].left, p_rct[i].top, p_rct[i].right, p_rct[i].bottom);
if (collision)
setfillcolor(GREEN);
solidcircle((int)ball.x, (int)ball.y, RADIUS);
}
int main()
{
initgraph(WIDTH, HEIGHT);
BeginBatchDraw();
srand((UINT)time(nullptr));
// 随机速度
ball.vx = fmodf((float)rand(), SPEED - rand() % 10 / 1000.f /* 增加扰动 */) * (rand() % 2 ? 1 : -1);
ball.vy = sqrtf(SPEED * SPEED - ball.vx * ball.vx) * (rand() % 2 ? 1 : -1);
// 初始位置
ball.x = (float)RADIUS + rand() % 20;
ball.y = (float)RADIUS + rand() % 20;
// 存储矩形碰撞箱
const int count = 8;
RECT p_rct[count] = {
{-10,-10,WIDTH + 10,-1}, // 边界
{-10,HEIGHT,WIDTH + 10,HEIGHT + 10}, // 边界
{-10,-1,-1,HEIGHT}, // 边界
{WIDTH,-1,WIDTH + 10,HEIGHT}, // 边界
// 矩形
{86,72,207,177},
{391,37,500,113},
{103,334,229,407},
{304,200,493,339}
};
while (true)
{
cleardevice();
bool collision = false;
// 一帧内运算多次
for (int k = 0; k < 3; k++)
{
for (int i = 0; i < count; i++)
if (BallCollisionProcess(p_rct[i]))
collision = true;
ball.x += ball.vx + rand() % 10 / 100.f /* 随机扰动 */;
ball.y += ball.vy + rand() % 10 / 100.f;
}
Render(p_rct, count, collision);
FlushBatchDraw();
Sleep(50);
}
EndBatchDraw();
closegraph();
return 0;
}
