TIN 三角网的生成

2020-3-31 ~ 2023-3-8
(0)
三角网的概念
三角网是由一系列连续三角形构成的网状的平面控制图形,是三角测量中布设连续三角形的两种主要扩展形式,同时向各方向扩展而构成网状,优点为点位分布均匀、各点之间互相牵制、图形强度较高,缺点是扩展较缓慢。
三角网是实现地形三维可视化,数字地面模型(Digital Terrain Model,简称 DTM)是一种很有效的途径。DTM 主要是由栅格和不规则三角网(Triangulated Irregular Network,简称 TIN )两种数据格式来表示,相比于栅格 TIN 具有许多优点,几乎能适用于任何复杂的地形,所以 TIN 是 DTM 常采用的一种格式。
三角网的特性
- TIN 是惟一的;
- 力求最佳的三角形几何形状,每个三角形尽量接近等边形状;
- 保证最邻近的点构成三角形,即三角形的边长之和最小;
- 最小角最大,即在所有的三角网中 Delaunay 三角网的最小角是相对最大的。狄洛尼三角网满足以上三个条件,其定义为 : 是相互邻接且互不重叠的三角形的集合,每一三角形的外接圆内不包含其他的点(空外接圆法则)。
书写 TIN 三角网的思路
首先生成一些随机点,在这些随机点中找到距离最短的两个点连线,以这条线拓展。然后就可以用循环语句判断所有的点,使每一个点与已经连线的这两个点构成外接圆(三个坐标点可以确定圆心和半径),判断圆内有没其他的点(依据圆的半径是否大于这个点到圆心的距离)如果圆内没有其他的点,就可以将这三个点连接一下,如果含有其他的点(及距离小于圆的半径)就停止本次循环,继续判断下一个点,当然,每次判断完后,都需要将判断成立的点与连接的线记录一下,循环的理念是用未连线的与已连线的点之间的判断。直至将所以的点都判断一遍,记录线的目的是为了防止重复画线。
运行效果:
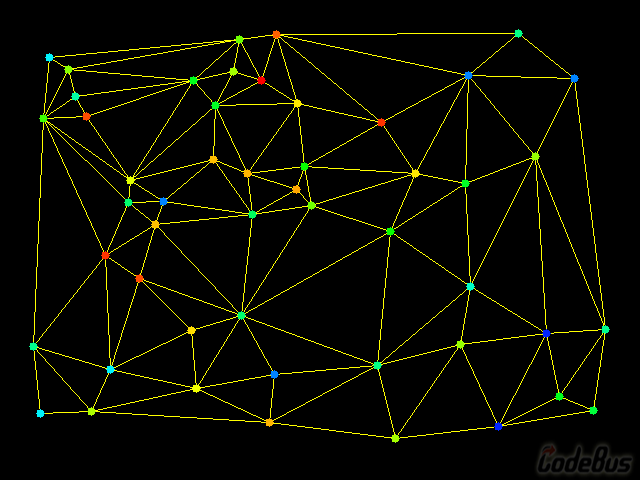
源码:
///////////////////////////////////////////////////
// 程序名称:TIN 三角网生成
// 编译环境:Mictosoft Visual Studio 2013, EasyX_20200315(beta)
// 作 者:luoyh <2864292458@qq.com>
// 最后修改:2020-4-1
// 用于生成 TIN 三角网实现外接圆算法
//
#include <graphics.h>
#include <math.h>
#include <stdio.h>
#include <conio.h>
#include <time.h>
#define WIDTH 640 // 生成窗口的大小
#define HEIGHT 480
#define NUMBER 50 // 随机点的个数
int X[NUMBER]; // 储存 X 方向产生的随机数
int Y[NUMBER]; // 储存 Y 方向产生的随机数
bool LineXY[(1 + NUMBER) * NUMBER / 2] = { false }; // 为了判断两点是否连线定义的一维数组
//判断这两个点是否连线
bool IsLinked(int p1, int p2)
{
if (p1 >= p2)
return LineXY[(1 + p1) * p1 / 2 + p2];
else
return LineXY[(1 + p2) * p2 / 2 + p1];
}
//储存已经绘制过的线
void Link(int p1, int p2)
{
if (p1>=p2)
LineXY[(1 + p1) * p1 / 2 + p2] = true;
else
LineXY[(1 + p2) * p2 / 2 + p1] = true;
}
// 绘制随机点
void drawpoint(int x, int y, float z)
{
float S = 1, L = 0.5;
setfillcolor(HSLtoRGB(z, S, L));
solidcircle(x, y, 4);
}
// 用于计算两点的距离
double distance(double x1, double y1, int x2, int y2)
{
return sqrt((double)((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)));
}
// 用于产生随机点
void Randompoint(int width, int height, int *lx, int *ly, int n)
{
int i;
bool T;
while (true)
{
i = 0;
*lx = (rand() % (width - 60) + 30);
*ly = (rand() % (height - 60) + 30);
while (true)
{
if (i >= n)
{
T = true;
break;
}
if (distance(*lx, *ly, X[i], Y[i]) < 20) // 用于控制随机点之间的距离
{
T = false;
break;
}
i++;
}
if (T == false)
continue;
else
break;
}
}
// 根据三个点坐标算出他们三个形成外接圆的圆心和半径
double CircleCenter(int x1, int y1, int x2, int y2, int x3, int y3, double *x, double *y, double *r)
{
if ((2.0 * (x1 * (y2 - y3) - y1 * (x2 - x3) + x2 * y3 - x3 * y2)) == 0)
{
*x = 0;
*y = 0;
*r = 0;
return *r;
}
*x = ((x1 * x1 + y1 * y1) * (y2 - y3) + (x2 * x2 + y2 * y2) * (y3 - y1) + (x3 * x3 + y3 * y3) * (y1 - y2)) / (2.0 * (x1 * (y2 - y3) - y1 * (x2 - x3) + x2 * y3 - x3 * y2));
*y = ((x1 * x1 + y1 * y1) * (x3 - x2) + (x2 * x2 + y2 * y2) * (x1 - x3) + (x3 * x3 + y3 * y3) * (x2 - x1)) / (2.0 * (x1 * (y2 - y3) - y1 * (x2 - x3) + x2 * y3 - x3 * y2));
*r = sqrt((*x - x1) * (*x - x1) + (*y - y1) * (*y - y1));
return *r;
}
int main()
{
initgraph(WIDTH, HEIGHT);
float G[NUMBER]; // 储存不同的颜色(后期可以用来储存高程
int Z[NUMBER]; // 储存判断过的点的数组
double max = WIDTH * HEIGHT * WIDTH; // 用窗口的长和宽来定义一个相对大的数
int lx; // 储存临时 X 方向产生的变量
int ly; // 储存临时 Y 方向产生的变量
int li; // 用于储存临时判断过的点的下标数
srand((unsigned)time(NULL)); // 初始化随机数
for (int i = 0; i < NUMBER; i++)
{
Randompoint(WIDTH, HEIGHT, &lx, &ly, i);
X[i] = lx; // 产生 X 方向的随机数
Y[i] = ly; // 产生 Y 方向的随机数
G[i] = float(rand() % 240); // 产生不同的颜色的随机数(后期可以用来表示高程)
drawpoint(X[i], Y[i], G[i]); // 绘制随机点
}
float H = 60, S = 1, L = 0.5;
setlinecolor(HSLtoRGB(H, S, L));
// 在随机生成的点中依次判断,找出距离最短的两个点
for (int i = 0; i < NUMBER; i++)
{
for (int j = i+1; j < NUMBER; j++)
{
if (max > distance(X[i], Y[i], X[j], Y[j]))
{
lx = i;
ly = j;
max = distance(X[i], Y[i], X[j], Y[j]);
}
}
}
line(X[lx], Y[lx], X[ly], Y[ly]);
Link(lx, ly);
Z[0] = lx;
Z[1] = ly;
int n = 2;
while (true)
{
if (n >= NUMBER)
break;
int m = 0;
double rad, Xd, Yd, Rd;
bool OK = false;
max = WIDTH * HEIGHT * WIDTH;
// 开始判断随机生成的每一个点
for (int i = 0; i < NUMBER; i++)
{
m = 0;
OK = false;
// 判断这个点是否已经判断过,如果已经判断过,返回判断下一个点,如果不在,继续程序
while (true)
{
if (m >= n)
{
m = 0;
break;
}
if (i == Z[m])
{
OK = true;
break;
}
m++;
}
if (OK == true)
continue;
// 在已经确定的两个点和未确定的点进行计算它们形成三角形的的半径,并判断形成的圆内有无其它的点
// 若无其它的点,则可以连线,如有其它的点,则进行判断下一个点
for (int j = 0; j < n; j++)
{
for (int k = 0; k < n; k++)
{
rad = CircleCenter(X[Z[j]], Y[Z[j]], X[Z[k]], Y[Z[k]], X[i], Y[i], &Xd, &Yd, &Rd);
int cc = 0;
OK = false;
while (true)
{
if (cc >= NUMBER)
break;
// 判断圆内有无其它点,并且这个被判断的点不能为形成这个圆的这个三个点,如果有其它点,就跳出该循环
if (distance(Xd, Yd, X[cc], Y[cc]) <= Rd && cc != Z[k] && cc != Z[j] && cc != i)
{
OK = true;
break;
}
cc++;
}
// 因为圆内有其它点,结束本次循环
if (OK == true)
continue;
if (max >= rad && rad !=0) // 在三个点围成圆内没有点找到半径最小的
{
lx = Z[j];
ly = Z[k];
if (rad >= WIDTH)
continue;
else
{
if (IsLinked(i, lx) == false) // 绘制线段,首先判断这个线段是否已经绘制过
{
Link(i, lx);
line(X[i], Y[i], X[lx], Y[lx]);
/*Sleep(100);*/ // 如果需要查看绘制过程,去掉注释
}
if (IsLinked(i, ly) == false)
{
Link(i, ly);
line(X[i], Y[i], X[ly], Y[ly]);
/*Sleep(100);*/ // 如果需要查看绘制过程,去掉注释
}
if (IsLinked(lx, ly) == false)
{
Link(lx, ly);
line(X[lx], Y[lx], X[ly], Y[ly]);
/*Sleep(100);*/ // 如果需要查看绘制过程,去掉注释
}
li = i;
}
}
}
}
}
Z[n] = li;
n++;
}
//重新描点
for (int i = 0; i < NUMBER; i++)
{
drawpoint(X[i], Y[i], G[i]);
}
_getch();
return 0;
}
作 者:鬼魅森林
Q Q: 2864292458
邮 箱:2864292458@qq.com

添加评论
取消回复