慢羊羊的空间

基于上篇文章 Mandelbrot Set (曼德布洛特集) 的源代码：
https://codebus.cn/yangw/mandelbrot-set

我修改了几个地方：

1. 修改了颜色，使用黑->蓝->白->棕->黑这样的渐变颜色方案（当然，可以修改 InitColor() 函数改变配色方案）

2. 增加了放大鼠标选中区域的功能。按鼠标中键可以恢复原尺寸。

3. 将迭代次数提了出来，定义了常量。如果需要绘制更精细的图，请加大常量 ITERATIONS。不过越大绘制的越慢。精细程度开始看不出来，放大次数多了就明显了。

4. 理论上是可以无穷放大，但实际受 double 类型精度的影响，放大到一定程度就会是马赛克了。

先看看逐步放大的效果吧：

另一个位置的逐步放大效果：

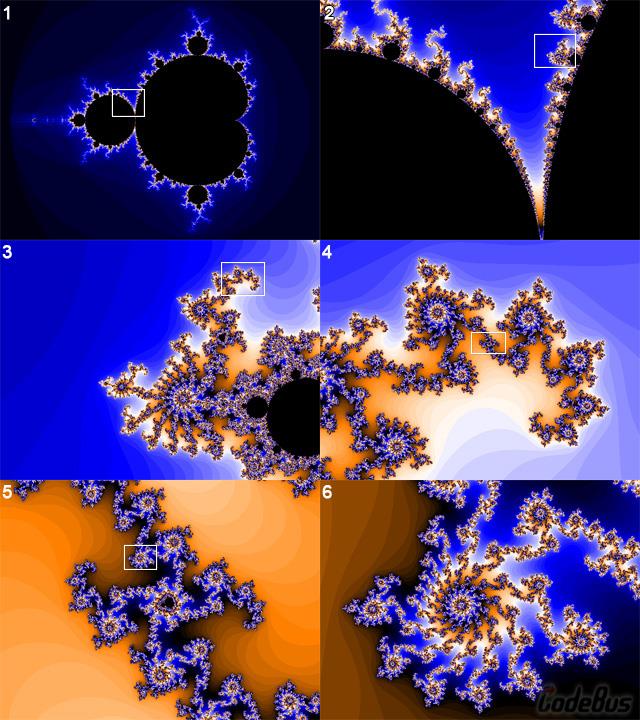
代码如下：

// 程序名称：分形学 - 可以无穷放大的 Mandelbrot Set (曼德布洛特集)
// 编译环境：Visual C++ 6.0 ~ 2019，EasyX_20210730
// 最后更新：2010-9-9
//
#include <graphics.h>
#include <conio.h>

// 定义常量
#define ITERATIONS 1000		// 迭代次数，越高，图像越精细
#define MAXCOLOR 64			// 颜色数


/////////////////////////////////////////////////
// 定义复数及乘、加运算
/////////////////////////////////////////////////

// 定义复数
struct COMPLEX
{
	double re;
	double im;
};

// 定义复数“乘”运算
COMPLEX operator * (COMPLEX a, COMPLEX b)
{
	COMPLEX c;
	c.re = a.re * b.re - a.im * b.im;
	c.im = a.im * b.re + a.re * b.im;
	return c;
}

// 定义复数“加”运算
COMPLEX operator + (COMPLEX a, COMPLEX b)
{
	COMPLEX c;
	c.re = a.re + b.re;
	c.im = a.im + b.im;
	return c;
}


/////////////////////////////////////////////////
// 定义颜色及初始化颜色
/////////////////////////////////////////////////

// 定义颜色
int Color[MAXCOLOR];

// 初始化颜色
void InitColor()
{
	// 使用 HSL 颜色模式产生角度 h1 到 h2 的渐变色
	int h1 = 240, h2 = 30;
	for (int i = 0; i < MAXCOLOR / 2; i++)
	{
		Color[i] = HSLtoRGB((float)h1, 1.0f, i * 2.0f / MAXCOLOR);
		Color[MAXCOLOR - 1 - i] = HSLtoRGB((float)h2, 1.0f, i * 2.0f / MAXCOLOR);
	}
}


/////////////////////////////////////////////////
// 绘制 Mandelbrot Set (曼德布洛特集)
/////////////////////////////////////////////////
void Draw(double fromx, double fromy, double tox, double toy)
{
	COMPLEX z, c;
	int x, y, k;	// 定义循环变量
	for (x = 0; x < 640; x++)
	{
		c.re = fromx + (tox - fromx) * (x / 640.0);
		for (y = 0; y < 480; y++)
		{
			c.im = fromy + (toy - fromy) * (y / 480.0);
			z.re = z.im = 0;
			for (k = 0; k < ITERATIONS; k++)
			{
				if (z.re * z.re + z.im * z.im > 4.0)	break;
				z = z * z + c;
			}
			putpixel(x, y, (k >= ITERATIONS) ? 0 : Color[k % MAXCOLOR]);
		}
	}
}


/////////////////////////////////////////////////
// 主函数
/////////////////////////////////////////////////
int main()
{
	// 初始化绘图窗口及颜色
	initgraph(640, 480);
	InitColor();


	// 初始化 Mandelbrot Set(曼德布洛特集)坐标系
	double fromx, fromy, tox, toy;
	fromx = -2.1; tox = 1.1;
	fromy = -1.2; toy = 1.2;
	Draw(fromx, fromy, tox, toy);


	// 捕获鼠标操作，实现放大鼠标选中区域
	ExMessage m;
	bool isLDown = false;
	int selfx, selfy, seltx, selty;	// 定义选区

	do
	{
		getmessage(&m, EM_MOUSE | EM_KEY);			// 获取一条鼠标消息

		switch (m.message)
		{
		case WM_KEYDOWN:
			break;

			// 按鼠标中键恢复原图形坐标系
		case WM_MBUTTONUP:
			fromx = -2.1; tox = 1.1;
			fromy = -1.2; toy = 1.2;
			Draw(fromx, fromy, tox, toy);
			break;

			// 按鼠标左键并拖动，选择区域
		case WM_MOUSEMOVE:
			if (isLDown)
			{
				rectangle(selfx, selfy, seltx, selty);
				seltx = m.x;
				selty = m.y;
				rectangle(selfx, selfy, seltx, selty);
			}
			break;

			// 按鼠标左键并拖动，选择区域
		case WM_LBUTTONDOWN:
			setlinecolor(WHITE);
			setrop2(R2_XORPEN);
			isLDown = true;
			selfx = seltx = m.x;
			selfy = selty = m.y;
			rectangle(selfx, selfy, seltx, selty);

			break;

			// 按鼠标左键并拖动，选择区域
		case WM_LBUTTONUP:
			rectangle(selfx, selfy, seltx, selty);
			setrop2(R2_COPYPEN);
			isLDown = false;
			seltx = m.x;
			selty = m.y;

			if (selfx == seltx || selfy == selty)	break;

			// 修正选区为 4:3
			int tmp;
			if (selfx > seltx) { tmp = selfx; selfx = seltx; seltx = tmp; }
			if (selfy > selty) { tmp = selfy; selfy = selty; selty = tmp; }

			if ((seltx - selfx) * 0.75 < (selty - selfy))
			{
				selty += (3 - (selty - selfy) % 3);
				selfx -= (selty - selfy) / 3 * 4 / 2 - (seltx - selfx) / 2;
				seltx = selfx + (selty - selfy) / 3 * 4;
			}
			else
			{
				seltx += (4 - (seltx - selfx) % 4);
				selfy -= (seltx - selfx) * 3 / 4 / 2 - (selty - selfy) / 2;
				selty = selfy + (seltx - selfx) * 3 / 4;
			}

			// 更新坐标系
			double f, t;
			f = fromx + (tox - fromx) * selfx / 640;
			t = fromx + (tox - fromx) * seltx / 640;
			fromx = f;
			tox = t;
			f = fromy + (toy - fromy) * selfy / 480;
			t = fromy + (toy - fromy) * selty / 480;
			fromy = f;
			toy = t;

			// 画图形
			Draw(fromx, fromy, tox, toy);

			break;
		}
	} while (m.message != WM_KEYDOWN);

	closegraph();
	return 0;
}