[译] 短小精悍又不可思议的数学艺术挑战赛及各路大神优秀作品展示

比赛简介
本文翻译了国外 StackExchange 上发起的一个叫做 Tweetable Mathematical Art 的比赛,该比赛以极为精简的 C++ 代码生成各种不可思议的图案。原比赛地址:https://codegolf.stackexchange.com/questions/35569/tweetable-mathematical-art。
参赛者需要写三个函数,根据坐标分别返回对应的红、蓝、绿数值:
// 红色
unsigned char RD(int i, int j)
{
// YOUR CODE HERE
}
// 绿色
unsigned char GR(int i, int j)
{
// YOUR CODE HERE
}
// 蓝色
unsigned char BL(int i, int j)
{
// YOUR CODE HERE
}
参数 i、j 表示 x、y 坐标,范围 0~1024,返回值范围 0~255。
例如:RD(100, 20) 返回 50,GR(100, 20) 返回 60,BL(100, 20) 返回 70,那么图像 100, 20 位置的颜色为 RGB(50, 60, 70)。
比赛要求是:每个函数的函数体,不超过 140 字符。程序框架提供了几个可以简化代码的定义,可以直接使用。
参赛者编写的三个函数会被插入到如下代码框架中(为了方便显示,我已经修改为 EasyX 绘图):
// 程序名称:Tweetable Mathematical Art 比赛的 EasyX 版本
// 原比赛地址:https://codegolf.stackexchange.com/questions/35569/tweetable-mathematical-art
//
#include <graphics.h>
#include <math.h>
#include <stdlib.h>
#include <time.h>
#define DIM 1024
#define DM1 (DIM-1)
#define _sq(x) ((x)*(x)) // 平方
#define _cb(x) abs((x)*(x)*(x)) // 立方的绝对值
#define _cr(x) (unsigned char)(pow((x),1.0/3.0)) // 立方根(运算结果取整)
unsigned char GR(int,int);
unsigned char BL(int,int);
unsigned char RD(int i, int j)
{
// YOUR CODE HERE
}
unsigned char GR(int i, int j)
{
// YOUR CODE HERE
}
unsigned char BL(int i, int j)
{
// YOUR CODE HERE
}
int main()
{
initgraph(1024, 1024);
srand((unsigned)time(NULL));
DWORD *p = GetImageBuffer(NULL);
for (int y = 0; y < 1024; y++)
for (int x = 0; x < 1024; x++)
// putpixel(x, y, RGB(RD(x, y), GR(x, y), BL(x, y))); // 逐步显示(慢)
p[(y << 10) + x] = RD(x, y) << 16 | GR(x, y) << 8 | BL(x, y); // 直接写显示缓冲区(快)
FlushBatchDraw();
getmessage(EX_CHAR); // 按任意键退出
closegraph();
return 0;
}
示例
将示例中的 RD、GR、BL 三个函数,替换到上面的代码框架中,编译执行,即可看到生成的效果图。
示例代码 1:
unsigned char RD(int i,int j)
{
unsigned short n = (unsigned short)sqrt((double)(_sq(i-DIM/2)*_sq(j-DIM/2))*2.0);
n &= DM1;
return (n >> 8 | n << 8) * 255 / 1023;
}
unsigned char GR(int i,int j)
{
unsigned short n = (unsigned short)sqrt((double)(
(_sq(i-DIM/2)|_sq(j-DIM/2))*
(_sq(i-DIM/2)&_sq(j-DIM/2))
));
n &= DM1;
return (n >> 8 | n << 8) * 255 / 1023;
}
unsigned char BL(int i,int j)
{
unsigned short n = (unsigned short)sqrt((double)(_sq(i-DIM/2)&_sq(j-DIM/2))*2.0);
n &= DM1;
return (n >> 8 | n << 8) * 255 / 1023;
}
生成效果:
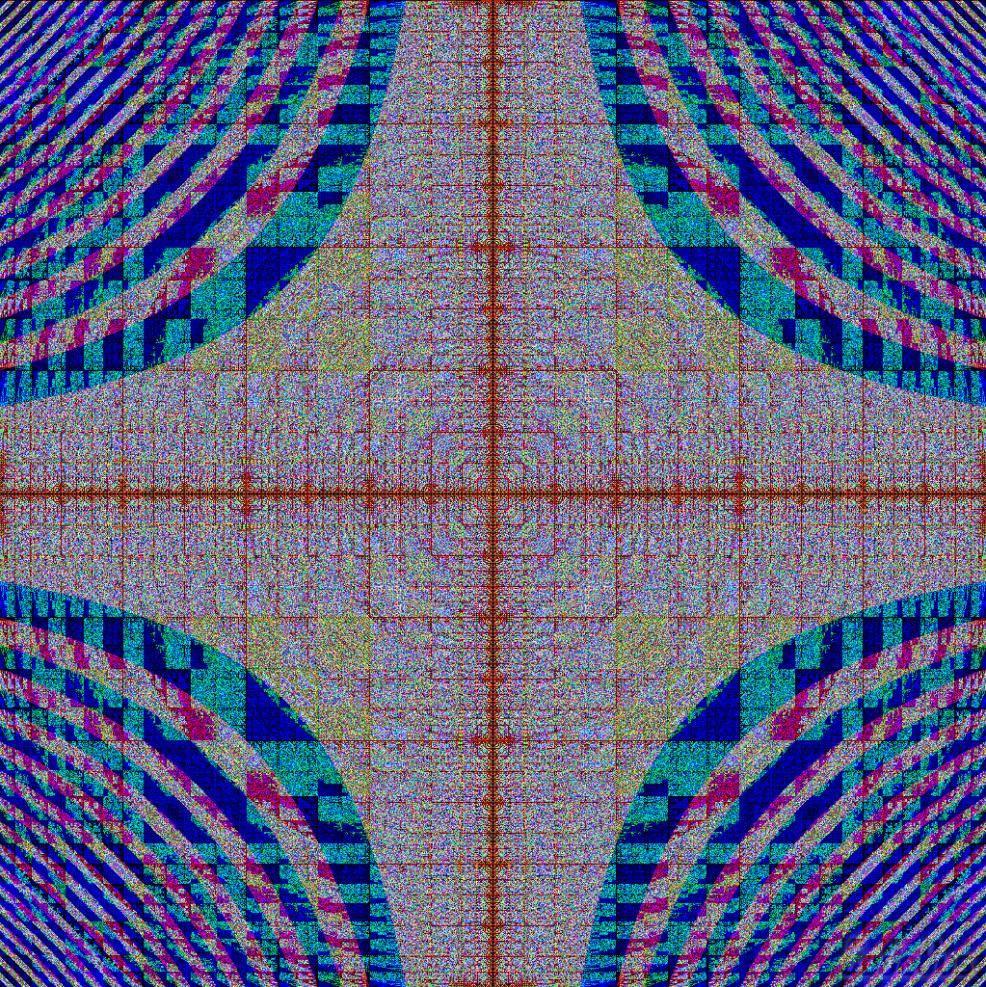
示例代码 2:
unsigned char RD(int i,int j)
{
unsigned short n = i&&j?(i%j)&(j%i):0;
n &= DM1;
return (n >> 8 | n << 8) * 255 / 1023;
}
unsigned char GR(int i,int j)
{
unsigned short n = i&&j?(i%j)+(j%i):0;
n &= DM1;
return (n >> 8 | n << 8) * 255 / 1023;
}
unsigned char BL(int i,int j)
{
unsigned short n = i&&j?(i%j)|(j%i):0;
n &= DM1;
return (n >> 8 | n << 8) * 255 / 1023;
}
生成效果:

各路大神的优秀作品
这个比赛引起了全球很多人的参与,以下是原文中各路大神的作品:
- 作品集 1:https://codebus.cn/yangw/tweetable-mathematical-art-1
- 作品集 2:https://codebus.cn/yangw/tweetable-mathematical-art-2
- 作品集 3:https://codebus.cn/yangw/tweetable-mathematical-art-3(更新中)
以下是国内大神的作品:
(更新中)
原比赛已经封贴,不再更新。如果你也有优秀的作品,请给我发消息,我把你的大作也加进来。
附注:关于原比赛的一点 bug
原比赛的代码框架如下:
// NOTE: compile with g++ filename.cpp -std=c++11
// also, if this doesn't work for you, try the alternate char-based version
#include <iostream>
#include <cmath>
#define DIM 1024
#define DM1 (DIM-1)
#define _sq(x) ((x)*(x)) // square
#define _cb(x) abs((x)*(x)*(x)) // absolute value of cube
#define _cr(x) (unsigned short)(pow((x),1.0/3.0)) // cube root
unsigned short GR(int,int);
unsigned short BL(int,int);
unsigned short RD(int i,int j){
// YOUR CODE HERE
}
unsigned short GR(int i,int j){
// YOUR CODE HERE
}
unsigned short BL(int i,int j){
// YOUR CODE HERE
}
void pixel_write(int,int);
FILE *fp;
int main(){
fp = fopen("MathPic","wb");
fprintf(fp, "P6\n%d %d\n1023\n", DIM, DIM);
for(int j=0;j<DIM;j++)
for(int i=0;i<DIM;i++)
pixel_write(i,j);
fclose(fp);
return 0;
}
void pixel_write(int i, int j){
static unsigned short color[3];
color[0] = RD(i,j)&DM1;
color[1] = GR(i,j)&DM1;
color[2] = BL(i,j)&DM1;
fwrite(color, 2, 3, fp);
}
框架里面提到的另一个 char 版本是没问题的,存在 bug 的是上面这个 short 版本。
对于 short 版本,原比赛的要求是,每个颜色分量为 10bit,返回值的范围为 [0, 1023],unsigned short 类型,将数据生成到一个 ppm 文件中,再以图片形式显示该文件。
但是,比赛使用 ppm 格式的 P6 编码,颜色数据以二进制形式存储,由于 Windows 和 Linux 存在字节序的差异,导致这里有一个严重的 bug。
例如,10bit 的红色分量返回值为 678,那么对应的 8bit 颜色值应该是:678 * 255 / 1023 = 169。
如果在 Windows 下写入 ppm 文件(P6 编码)并在 Linux 下读取显示 ppm 时,该颜色分量的值会进行如下转换:678 转为 16 进制=> 0x2A6 高低位交换=> 0xA602 转为 10 进制=> 42498 计算=> 42498 * 255 / 1023 = 10593 保存到 8bit 变量中=> 10593 & 0xff = 97。显然,这个差距是巨大且无法接受的。
而该比赛给出的范例,恰恰是利用了这样的 bug 才能得出原文给出的效果。
- 如果在 Windows 下生成 ppm(P6 编码)并在 Windows 下查看,无法得出指定效果。
- 如果在 Linux 下生成 ppm(P6 编码)并在 Linux 下查看,无法得出指定效果。
- 如果在 Windows 下生成 ppm(P3 编码,ASCII 格式)并在 Linux 下查看,无法得出指定效果。
本文在将代码转换成 EasyX 时,对于使用 char 版本框架的代码,无需修改,可以直接使用。对于使用 short 版本框架的代码,为了达成原图效果,需要加几行代码模拟这个 bug,例如原文代码:
unsigned char RD(int i,int j)
{
return i&&j?(i%j)&(j%i):0;
}
需要修改为:
unsigned char RD(int i,int j)
{
unsigned short n = i&&j?(i%j)&(j%i):0;
n &= DM1;
return (n >> 8 | n << 8) * 255 / 1023;
// return n * 255 / 1023; // 有些参赛选手的代码在 Linux 下编译,无需交换高低位,就用这行代码替代上一行
}
这样有可能使代码超出 140 字节,望悉知。

添加评论
取消回复