桃树

 童老师的樱花树令人印象深刻,今天闲来无事,尝试着把递归改成了循环,把开花的方式稍加修改,得到了一颗稍微不一样的一棵树,看起来像是一颗桃树?
童老师的樱花树令人印象深刻,今天闲来无事,尝试着把递归改成了循环,把开花的方式稍加修改,得到了一颗稍微不一样的一棵树,看起来像是一颗桃树?
 童老师的樱花树令人印象深刻,今天闲来无事,尝试着把递归改成了循环,把开花的方式稍加修改,得到了一颗稍微不一样的一棵树,看起来像是一颗桃树?
童老师的樱花树令人印象深刻,今天闲来无事,尝试着把递归改成了循环,把开花的方式稍加修改,得到了一颗稍微不一样的一棵树,看起来像是一颗桃树?

关于 Julia Set (茱莉亚集) 的介绍什么的我就不多说了,网上一大堆。执行效果如图:
关于 Julia Set,可以通过设置复数 c 的初值,显示出不同的图案,比如,大家可以试试以下几组:
c.re = 0.45, c.im = -0.1428; c.re = 0.285, c.im = 0.01; c.re = 0.285, c.im = 0; c.re = -0.8, c.im = 0.156; c.re = -0.835, c.im = -0.2321; c.re = -0.70176, c.im = -0.3842;
随便用哪行替换掉源程序中的“c.re = -0.75, c.im = 0;”都可以看到不同的精美图案。循环变量 k 是迭代次数,在某些参数下需要高一些会更精细。
为了美观,还需要修改一下颜色部分,目前代码中的颜色是这样的:
...HSLtoRGB((float)((k<<5) % 3
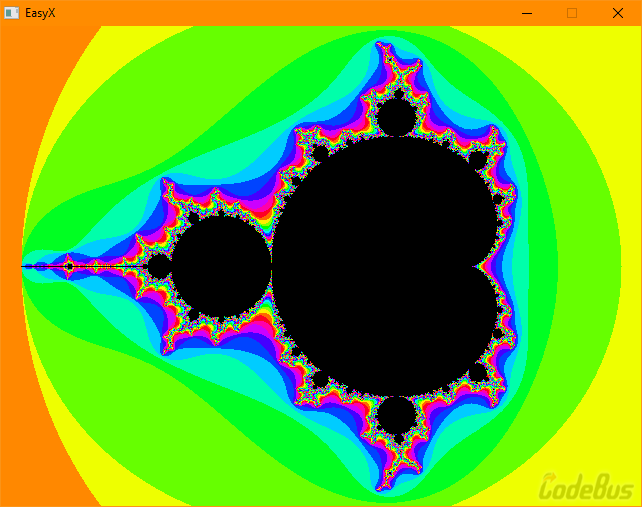
关于 Mandelbrot Set (曼德布洛特集) 的介绍什么的我就不多说了,网上一大堆。执行效果如图:
为了美观,可以修改一下颜色部分,目前代码中的颜色是这样的:
HSLtoRGB((float)((k<<5) % 360), 1.0, 0.5)
这行代码中的 k 的取值范围是 0~180,将其映射到 HSL 颜色空间中的色相上(360 度)。
全部代码如下:
// 程序名称:分形学 - Mandelbrot Set (曼德布洛特集)
// 编译环境:Visual C++ 6.0,EasyX_20200902
// 最后更新:2010-9-9
//
#include <graphics.h>
#include <conio.h>
/////////////////////////////////////////////////
// 定义复数及乘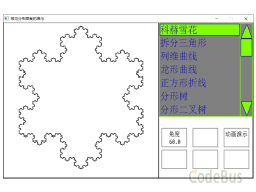 这个程序包含了一些常见分形图案的动画演示,并提供了一些按钮来改变有意义的可变变量,创造不一样的分形图案。
这个程序包含了一些常见分形图案的动画演示,并提供了一些按钮来改变有意义的可变变量,创造不一样的分形图案。
 EasyIFS 是开源的分形学 IFS 演示程序。该程序可以依据 IFS 数据文件中定义的参数,生成图像。
EasyIFS 是开源的分形学 IFS 演示程序。该程序可以依据 IFS 数据文件中定义的参数,生成图像。

德国数学家 David Hilbert 发现了这样一种可以填满整个单位正方形的分形曲线,称它为 Hilbert 曲线。具体的我就不多做介绍了,相关内容请自己搜索。这里只说程序。
程序执行后,按数字键 1~8 可以显示相应阶数的 Hilbert (希尔伯特) 曲线,按 ESC 退出。
五阶 Hilbert (希尔伯特) 曲线的执行效果如下:
代码如下:
// 程序名称:Hilbert (希尔伯特)曲线 (基于 L 系统绘制)
// 编译环境:Visual C++ 6.0,EasyX 2011惊蛰版
// 最后修改:2011-3-7
//
#include <graphics.h>
#include <conio.h>
int g_len; // Hilbert 曲线的单位长度
// 递归绘制 Hilbert 曲线
void hilbert(LPCTSTR cmd, int level)
{
static BYTE d = 
基于上篇文章 Mandelbrot Set (曼德布洛特集) 的源代码:
https://codebus.cn/yangw/mandelbrot-set
我修改了几个地方:
修改了颜色,使用黑->蓝->白->棕->黑这样的渐变颜色方案(当然,可以修改 InitColor() 函数改变配色方案)
增加了放大鼠标选中区域的功能。按鼠标中键可以恢复原尺寸。
将迭代次数提了出来,定义了常量。如果需要绘制更精细的图,请加大常量 ITERATIONS。不过越大绘制的越慢。精细程度开始看不出来,放大次数多了就明显了。
理论上是可以无穷放大,但实际受 double 类型精度的影响,放大到一定程度就会是马赛克了。
先看看逐步放大的效果吧:
另一个位置的逐步放大效果:
代码如下:
...
分形几何学是一门以不规则几何形态为研究对象的几何学。一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统。虽然分形是一个数学构造,它们同样可以在自然界中被找到,这使得它们被划入艺术作品的范畴。
计算机协助了人们推开分形几何的大门。法国数学家曼德尔勃罗特这位计算机和数学兼通的人物,开创了新的数学分支——分形几何学。分形在医学、土力学、地震学和技术分析中都有应用。
毕达哥拉斯树(Pythagoras tree)是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的图形。又因为重复数次后的形状好似一棵树,所以被称为毕达哥拉斯树,也叫“勾股树”。
这个程序,展示了毕达哥拉斯树的生成。执行效果如下:
我的求解思路是:
先说一个程序的实现过程:
这个程序很简单,虽然随机性很大,但是结果几乎是完全相似的,会是一个很有趣的图案,也就是传说中的谢宾斯基三角形。以上步骤就是生成谢宾斯基三角形的随机迭代法。
程序代码如下:
(注:为了效果,将步骤(1)的三个点手动指定了。喜欢的话,可以将其修改为随机产生)。
// 程序名称:谢宾斯基(Sierpinski)三角形,也叫垫片
// 编译环境:Visual C++ 6.0,EasyX 2011惊蛰版
// 最后更新:2010-11-16
//
#include <graphics.h>
#include <